题目内容
5. 如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )| A. | 小球在最高点的最小速度为$\sqrt{gR}$ | |
| B. | 小球在最低点的最小速度为$\sqrt{5gR}$ | |
| C. | 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力 | |
| D. | 小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力 |
分析 圆形管道内能支撑小球,小球能够通过最高点时的最小速度为0.小球从最低点运动到最高点的过程中,只有重力做功,其机械能守恒.根据机械能守恒求出最低点的最小速度.由牛顿第二定律求出小球受到的管道的作用力大小和方向.
解答 解:A、由于圆形管道能支撑小球,所以小球能够通过最高点时的最小速度为0.故A错误.
B、小球通过最高点时的最小速度为0,根据机械能守恒得:mg2R=$\frac{1}{2}m{v}^{2}$
可得最低点的最小速度为:v=$2\sqrt{gR}$,故B错误.
C、小球在水平线ab以上的管道中运动时,设小球的速度为v,管道对小球的弹力大小为F,方向指向圆心,半径与竖直方向的夹角为α.小球经过最高点的速度为v′.由牛顿第二定律得:
mgcosα+F=m$\frac{{v}^{2}}{R}$
根据机械能守恒得:mgR(1-cosα)=$\frac{1}{2}{mv}^{2}-\frac{1}{2}mv{′}^{2}$
联立得:F=2mg(1-2cosα)-m$\frac{v{′}^{2}}{R}$可知F可能为正,也可能为负,所以外侧管壁对小球可能有作用力.故C错误.
D、在a点,小球所需要的向心力是由轨道外侧管壁的弹力提供的,所以可知小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力.故D正确.
故选:D
点评 本题中圆管模型与轻杆模型相似,抓住两个临界条件:一是小球恰好到达最高点时,速度为零;二是小球经过最高点与管道恰好无作用力时速度为$\sqrt{gR}$.

练习册系列答案
相关题目
15.物体在某一运动过程中,重力做功20J,则下列说法一定正确的是( )
| A. | 重力势能增加了20 J | B. | 重力势能减小了20 J | ||
| C. | 动能减小了20 J | D. | 动能增加了20 J |
20.关于功和能,下列说法不正确的是( )
| A. | 滑动摩擦力对物体可以做正功 | |
| B. | 当作用力对物体做正功时,反作用力可以不做功 | |
| C. | 做曲线运动的物体,由于速度不断地变化,一定有外力对物体做功 | |
| D. | 只受重力作用的物体,在运动过程中机械能一定守恒 |
17.如图所示是光的双缝干涉的示意图,下列说法中正确的是( )


| A. | 单缝S的作用是为了增加光的强度 | |
| B. | 当S1、S2发出两列光波到P点的路程差为光的波长λ的0.5倍时,产生第二暗条纹 | |
| C. | 双缝S1、S2的作用是为了产生两个频率相同的线状光源 | |
| D. | 当S1、S2发出的两列光波到P点的路程差为波长λ时,产生中央亮条纹 |
15.某电工用两根轻绳安装一盏电灯,由于安装不当,安装如图所示,轻绳长度AO<BO,则( )


| A. | AO绳和BO绳承受的拉力一样大 | B. | AO绳承受的拉力较大 | ||
| C. | BO绳承受的拉力较大 | D. | 电灯的重力一定大于绳子的拉力 |
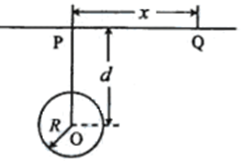 如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.设球形空腔体积为V,球心深度为d(远小于地球半径),$\overline{PQ}$=x,求:
如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.设球形空腔体积为V,球心深度为d(远小于地球半径),$\overline{PQ}$=x,求: 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求: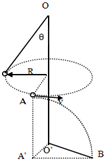 如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求:
如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求: