题目内容
4.一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )
| A. | 不论波向x轴哪一方向传播,在这0.5s内,x=1m处的质点M通过的路程都相等 | |
| B. | 当波向+x方向传播时,波速等于10m/s | |
| C. | 当波沿+x方向传播时,x=1m处的质点M和x=2.5m处的质点N在这0.5s内通过的路程相等 | |
| D. | 当波沿-x方向传播时,经过0.1s时,质点M的位移一定为零 |
分析 已知两个时刻的波形,波的传播方向可能沿向右,也可能向左.当波向右传播时,传播的最短距离是$\frac{1}{4}$波长,当波向左传播时,传播的最短距离是$\frac{3}{4}$波长,根据时间与周期的关系,求出周期,再求频率和波速及运动的位移和路程.
解答 解:A、当波沿-x方向传播时,0.5s=(0.75+n)T,当n=1时符合条件,解得T=$\frac{2}{7}$s,在这0.5s内,x=1m处的质点M通过的路程sM′=$\frac{0.5}{\frac{2}{7}}×4A=7A$,
当波沿+x方向传播时,0.5s=(0.25+n)T,当n=1时符合条件,解得T=0.4s,在这0.5s内,x=1m处的质点M通过的路程sM′=$\frac{0.5}{0.4}×4A=5A$,所以通过的路程不相同,故A错误,
B、由图线可直接读出波长λ=4m.因为0.25s<T<0.5s,
所以当波向+x方向传播时,0.5s=(0.25+n)T,当n=1时符合条件,解得T=0.4s,所以v=$\frac{λ}{T}=\frac{4}{0.4}=10m/s$,故B正确;
C、在这0.5s内,x=1m处的质点M通过的路程sM=5A=10cm,x=2.5m处的质点N在前0.4s内通过的路程为4,后0.1s内向上运动,平均速度比从位移最大处运动的平均速度大,所以在后0.1s内的路程大于A,所以在这0.5s内通过的路程sN>5A,故C错误;
D、当波沿-x方向传播时,T=$\frac{2}{7}$s,而$\frac{1}{2}T>$0.1s$>\frac{1}{4}T$,质点M没有回到平衡位置,位移不为零,故D错误
故选:B
点评 本题是利用波的时间周期性,求出周期,再求解波速的,也可以根据空间的周期性,求出波传播距离的通项,再求解波速,注意0.25s<T<0.5s,这个条件的应用.

| A. | 物体因为圆周运动才受到向心力 | |
| B. | 向心力不改变圆周运动物体速度的大小 | |
| C. | 作匀速圆周运动的物体其向心力是不变的 | |
| D. | 向心力就是做圆周运动的物体所受到的合外力 |
| A. | 重力势能增加了20 J | B. | 重力势能减小了20 J | ||
| C. | 动能减小了20 J | D. | 动能增加了20 J |
| A. | 恒力作用下的物体的运动不可能是曲线运动 | |
| B. | 变力作用下的物体的运动一定是曲线运动 | |
| C. | 匀速圆周运动是非匀变速运动 | |
| D. | 平抛是匀变速运动 |
| A. | 它们的线速度比vA:vB=1:1 | B. | 它们的向心加速度比2:3 | ||
| C. | 它们的周期比TA:TB=2:3 | D. | 它们的周期比TA:TB=1:2 |
 如图的装置中,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,两轨道上分别装有电磁铁C、D;调节电磁C、D的高度,使AC=BD,从而保证小铁球P、Q在轨道出口处的水平初速度v0相等.将小铁球P、Q分别吸到电磁铁上,然后切断电源,使两小铁球以相同的初速度从轨道M、N下端口射出,实验结果是两小球同时到达E处,发生碰撞.现在多次增加或减小轨道M口离水平面BE的高度(即只改变P球到达水平面速度的竖直分量大小),再进行实验的结果是:
如图的装置中,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,两轨道上分别装有电磁铁C、D;调节电磁C、D的高度,使AC=BD,从而保证小铁球P、Q在轨道出口处的水平初速度v0相等.将小铁球P、Q分别吸到电磁铁上,然后切断电源,使两小铁球以相同的初速度从轨道M、N下端口射出,实验结果是两小球同时到达E处,发生碰撞.现在多次增加或减小轨道M口离水平面BE的高度(即只改变P球到达水平面速度的竖直分量大小),再进行实验的结果是: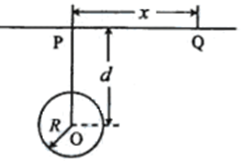 如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.设球形空腔体积为V,球心深度为d(远小于地球半径),$\overline{PQ}$=x,求:
如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.设球形空腔体积为V,球心深度为d(远小于地球半径),$\overline{PQ}$=x,求: 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求: