题目内容
1.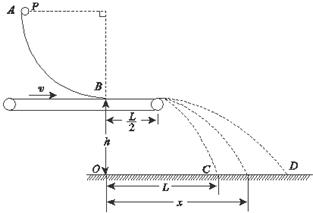 如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求:
如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求:(1)物体P与传送带之间的动摩擦因数;
(2)若在A处给物体P一个竖直向下的初速度v0,物体P从传送带的右端水平飞出后,落在地面上的D点,求OD的大小;
(3)若传送带驱动轮顺时针转动,带动传送带以速度v匀速运动,再把物体P从A处由静止释放,物体P落到地面上.设着地点与O点的距离为x,求出x与传送带上表面速度v的函数关系.
分析 (1)先研究无传送带的情况:物体从B运动到C,做平抛运动,已知h和L,由平抛运动的规律求得物体在B点的速度vB,再研究有传送带的情况:由平抛运动的规律求出物体离开传送带时的速度v1,根据动能定理求得摩擦因数μ.
(2)根据动能定理研究物体离开传送带时的速度,由平抛运动的知识求得OD.
(3)通过物体P滑到底端的速度与传送带的速度进行比较,判断物体P在传送带上的运动情况,得出物体离开传送带的速度,根据平抛运动的知识求出水平位移.
解答 解:(1)无传送带时,物体从B运动到C,做平抛运动,设物体在B点的速度为vB,
由L=vBt;
h=$\frac{1}{2}$gt2,
解得:vB=L$\sqrt{\frac{g}{2h}}$
当有传送带时,设物体离开传送带时的速度为v1,由平抛规律:
$\frac{L}{2}$=v1t
h=$\frac{1}{2}$gt2
解得:v1=L$\sqrt{\frac{g}{8h}}$;
由此可知物体滑上传送带时的初速度为vB,末速度为v1,物体的位移为$\frac{L}{2}$,此过程中只有传送带的摩擦力对物体做功,故根据动能定理有:
-μmg$\frac{L}{2}$=$\frac{1}{2}$m${v}_{1}^{2}$-$\frac{1}{2}$m${v}_{B}^{2}$
代入vB和v1可解得:
μ=$\frac{3L}{8h}$;
(2)设物体离开传送带时的速度为v2,物体从A滑到离开传送带的过程中,只有重力和传送带的摩擦力对物体做功,由动能定理有:
mgR-μmg$\frac{L}{2}$=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$
又物体从A滑至B的过程中有:
mgR=$\frac{1}{2}$m${v}_{B}^{2}$
所以有:
$\frac{1}{2}$m${v}_{B}^{2}$-$\frac{3L}{8h}$×mg$\frac{L}{2}$=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$
又vB=L$\sqrt{\frac{g}{2h}}$
可解得:v2=$\sqrt{\frac{g{L}^{2}}{8h}+{v}_{0}^{2}}$
物体离开传送带后做平抛运动,由题意根据平抛可知
OD=$\frac{L}{2}$+v2t=$\frac{L}{2}$+$\sqrt{\frac{g{L}^{2}}{8h}+{v}_{0}^{2}}$$\sqrt{\frac{2h}{g}}$=$\frac{L}{2}$+$\sqrt{\frac{{L}^{2}}{4}+\frac{2h{v}_{0}^{2}}{g}}$;
(3)物体由静止从P点开始下滑,到达B点的速度:
vB=L$\sqrt{\frac{g}{2h}}$,
当物体滑上传送带全程加速时,物体滑离传送带时的速度v2,根据动能定理有:
加速时摩擦力做正功,故有:
μmg$\frac{L}{2}$=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}$m${v}_{B}^{2}$
代入数值可得:
v2=$\sqrt{\frac{7g{L}^{2}}{8h}}$
所以当传送带的速度v>$\sqrt{\frac{7g{L}^{2}}{8h}}$,物体离开传送带的速度v>$\sqrt{\frac{7g{L}^{2}}{8h}}$,由题意根据平抛运动知识可知:
x=$\frac{L}{2}$+v2t=$\frac{L}{2}$+$\sqrt{{L}^{2}+\frac{3}{4}{L}^{2}}$=$\frac{L}{2}$(1+$\sqrt{7}$)
同理有当物体由静止从P点开始下滑,达到B点的速度vB=L$\sqrt{\frac{g}{2h}}$,当物体滑上传送带并在全程在摩擦力作用下做减速运动时,物体滑离传送带的时的速度为v1,根据动能定理有:
减速时摩擦力做负功,故有:-μmg$\frac{L}{2}$=$\frac{1}{2}$m${v}_{1}^{2}$-$\frac{1}{2}$m${v}_{B}^{2}$
代入相应数值可解得:v1=$\sqrt{\frac{g{L}^{2}}{8h}}$
所以当传送带速度小于v<$\sqrt{\frac{g{L}^{2}}{8h}}$时,物体滑离传送带时的速度v1=$\sqrt{\frac{g{L}^{2}}{8h}}$
所以可知;x=$\frac{L}{2}$+v1t=$\frac{L}{2}$+$\sqrt{\frac{g{L}^{2}}{8h}}$$\sqrt{\frac{2h}{g}}$=L
当传送带的速度满足:v1≤v≤v2时,物体在摩擦力作用下离开传送带时的速度大小都为v,
故此时x=$\frac{L}{2}$+v$\sqrt{\frac{2h}{g}}$
答:(1)物体P与传送带之间的摩擦因数μ=$\frac{3L}{8h}$;
(2)若在A处给物体P一个竖直向下的初速度,物体P从传送带的右端水平飞出后,落到地面上的D点,OD的大小为$\frac{L}{2}$+$\sqrt{\frac{{L}^{2}}{4}+\frac{2h{v}_{0}^{2}}{g}}$;
(3)若驱动轮转动、带动传送带以速度v匀速运动,再把物体P从A处由静止释放,物体P落到地面上,设着地点与O点的距离为x,x与传送带上表面速度v的函数关系为:
1、x=L时,v<$\sqrt{\frac{g{L}^{2}}{8h}}$;
2、x=$\frac{L}{2}$+v$\sqrt{\frac{2h}{g}}$时,$\sqrt{\frac{g{L}^{2}}{8h}}$≤v≤$\sqrt{\frac{7g{L}^{2}}{8h}}$;
3、x=$\frac{L}{2}$(1+$\sqrt{7}$)时,v>$\sqrt{\frac{7g{L}^{2}}{8h}}$.
点评 本题是机械能守恒、平抛运动,动能定理的综合应用,要具有分析物体运动过程的能力,能分情况全面分析物体的运动情况,要抓住平抛运动的时间由高度决定这一知识点.本题较难,易犯考虑不全面的错误.

 阅读快车系列答案
阅读快车系列答案| A. | 光传感器和红外线传感器,与门电路 | |
| B. | 光传感器和红外线传感器,或门电路 | |
| C. | 光传感器和声传感器,与门电路 | |
| D. | 光传感器和超声波传感器,或门电路 |
| A. | 恒力作用下的物体的运动不可能是曲线运动 | |
| B. | 变力作用下的物体的运动一定是曲线运动 | |
| C. | 匀速圆周运动是非匀变速运动 | |
| D. | 平抛是匀变速运动 |
| A. | 它们的线速度比vA:vB=1:1 | B. | 它们的向心加速度比2:3 | ||
| C. | 它们的周期比TA:TB=2:3 | D. | 它们的周期比TA:TB=1:2 |
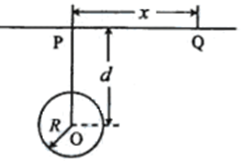 如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.设球形空腔体积为V,球心深度为d(远小于地球半径),$\overline{PQ}$=x,求:
如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.设球形空腔体积为V,球心深度为d(远小于地球半径),$\overline{PQ}$=x,求: 如图是宇航员在地面上空进行“太空行走”的情景,当他出舱后相对飞船静止不动时,他处于失重(选填超重、失重、平衡)状态;现已知地球的半径R和引力常数G,若想要根据万有引力提供飞船做圆周运动的向心力来计算地球的质量,还需要知道该飞船的哪些运动信息:周期T、与地面的高度h(写出相关物理量及对应的物理符号).
如图是宇航员在地面上空进行“太空行走”的情景,当他出舱后相对飞船静止不动时,他处于失重(选填超重、失重、平衡)状态;现已知地球的半径R和引力常数G,若想要根据万有引力提供飞船做圆周运动的向心力来计算地球的质量,还需要知道该飞船的哪些运动信息:周期T、与地面的高度h(写出相关物理量及对应的物理符号). 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求: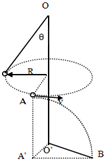 如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求:
如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求: