函数y=log
(x2-2x-3)的单调递增区间是( )
| 1 |
| 2 |
| A、(3,+∞) |
| B、(1,+∞) |
| C、(-∞,-1) |
| D、(-∞,1) |
函数f(x)=kx2+(3k-2)x-5在[1,+∞)上单调递增,则k的取值范围是( )
| A、(0,+∞) | ||
B、(-∞,
| ||
C、[
| ||
D、[
|
若函数f(x)=
在区间[-m,m]上是单调递增函数,则m的取值范围是( )
| 4x |
| x2+1 |
| A、m≤1 | B、m≥1 |
| C、0<m<2 | D、0<m≤1 |
已知函数f(x)是定义域为R的偶函数,且f(x+1)=-f(x),若f(x)在[-1,0]上是增函数,那么f(x)在[1,3]上是( )
| A、增函数 | B、减函数 | C、先增后减的函数 | D、先减后增的函数 |
如图给出的四个对应关系,其中构成映射的是( )
A、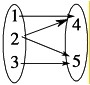 | B、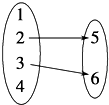 | C、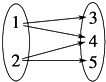 | D、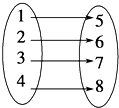 |
已知f(x)为定义在R上的奇函数,当x≥0时,f(x)=x(1+x),则当x<0时,有( )
| A、f(x)=-x(1+x) | B、f(x)=-x(1-x) | C、f(x)=x(1-x) | D、f(x)=x(x-1) |
函数y=
的图象大致为( )
| 3xcos3x |
| 9x-1 |
A、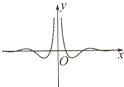 |
B、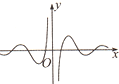 |
C、 |
D、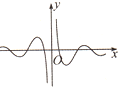 |
已知函数f(x)满足:f(x+1)和f(x-1)都是偶函数,当x∈[-1,1)时f(x)=|log2|x-1||,则下列说法错误的是( )
| A、函数f(x)在区间[3,4]上单调递减 | B、函数f(x)没有对称中心 | C、方程f(x)=k(k≥0)在x∈[-2,4]上一定有偶数个解 | D、函数f(x)存在极值点x0,且f′(x0)=0 |