题目内容
函数y=
的图象大致为( )
| 3xcos3x |
| 9x-1 |
A、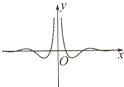 |
B、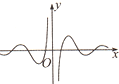 |
C、 |
D、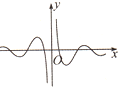 |
分析:求出函数的定义域,通过函数的定义域,判断函数的奇偶性及各区间上函数的符号,进而利用排除法可得答案.
解答:解:函数y=
的定义域为(-∞,0)∪(0,+∞),
且f(-x)=
=-
=-f(x)
故函数为奇函数,图象关于原点对称,故A错误
由分子中cos3x的符号呈周期性变化,故函数的符号也呈周期性变化,故C错误;
不x∈(0,
)时,f(x)>0,故B错误
故选:D
| 3xcos3x |
| 9x-1 |
且f(-x)=
| 3-xcos(-3x) |
| 9-x-1 |
| 3xcos3x |
| 9x-1 |
故函数为奇函数,图象关于原点对称,故A错误
由分子中cos3x的符号呈周期性变化,故函数的符号也呈周期性变化,故C错误;
不x∈(0,
| π |
| 6 |
故选:D
点评:本题考查函数的图象的综合应用,对数函数的单调性的应用,考查基本知识的综合应用,考查数形结合,计算能力.判断图象问题,一般借助:函数的定义域、值域、单调性、奇偶性、周期性、以及函数的图象的变化趋势等等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
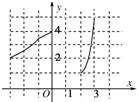 13、函数y=f(x)的图象如图所示.那么,f(x)的定义域是
13、函数y=f(x)的图象如图所示.那么,f(x)的定义域是