已知椭圆
+
=1 (a>b>0)的面积为abπ,若全集U={(x,y)|x∈R,y∈R},
集合A={(x,y)|
+
≤1},B={(x,y)|3x+4y+12>0},则A∩(?uB)所表示的图形的面积为( )
| x2 |
| a2 |
| y2 |
| b2 |
集合A={(x,y)|
| x2 |
| 16 |
| y2 |
| 9 |
| A、6(π-1) |
| B、9π+6 |
| C、3π-3 |
| D、3(π-2) |
曲线x-y=0,y=x2-2x,所围成的图形的面积是( )
| A、1 | ||
B、
| ||
| C、9 | ||
D、
|
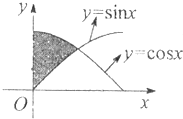
如图中阴影部分区域的面积S=( )

A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=
,直线x=-2,x=-1及x轴围成的区域的面积为( )
| 1 |
| x |
A、ln
| ||
| B、ln2 | ||
| C、ln3 | ||
| D、2ln2 |
曲线y=ex,x=0,x=1与x轴围成的面积为( )
| A、e2-1 | ||
| B、e-1 | ||
| C、e2 | ||
D、
|
若S1=
cosxdx,S2=
dx,S3=
exdx,则S1,S2,S3的大小关系是( )
| ∫ |
0 |
| ∫ | 2 1 |
| 1 |
| x |
| ∫ | 2 1 |
| A、S1<S2<S3 |
| B、S2<S1<S3 |
| C、S2<S3<S1 |
| D、S3<S2<S1 |
已知函数y=f(x)是R上的偶函数,且在区间(-∞,0)是单调递增的,若S1=
x2dx,S2=
dx,S3=
exdx则下列不等式中一定成立的是( )
| ∫ | 2 1 |
| ∫ | 2 1 |
| 1 |
| x |
| ∫ | 2 1 |
| A、f(S1)<f(S2)<f(S3) |
| B、f(S3)<f(S2)<f(S1) |
| C、f(S2)<f(S1)<f(S3) |
| D、f(S3)<f(S1)<f(S2) |
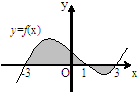 图中由函数y=f(x)图象与x轴围成的阴影部分面积,用定积分可表示为
图中由函数y=f(x)图象与x轴围成的阴影部分面积,用定积分可表示为