题目内容

若S1=
∫
π
2
0
cosxdx，S2=
∫
2
1
1
x
dx，S3=
∫
2
1
exdx，则S1，S2，S3的大小关系是（　　）
A、S1＜S2＜S3
B、S2＜S1＜S3
C、S2＜S3＜S1
D、S3＜S2＜S1
分析：根据积分公式分别计算S1，S2，S3的值，即可比较大小．
解答：解：S1=
∫
π
2
0
cosxdx=sinx|
 
π
2
0
=sin
π
2
-sin0=1，
S2=
∫
2
1
1
x
dx=lnx|
 
2
1
=ln2-ln1=ln2＜1，
S3=
∫
2
1
exdx=ex
|
2
1
=e2-e＞1，
则S2＜S1＜S3．
故选：B．
点评：本题主要考查积分的计算，要求熟练掌握常见函数的积分公式．
练习册系列答案
相关题目
精英家教网如图，设点P从原点沿曲线y=x2向点A（2，4）移动，记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1，S2，若S1=S2，求点P的坐标．
已知在区间（a，b）上，f（x）＞0，f′（x）＞0，对x轴上的任意两点（x1，0），（x2，0），（a＜x1＜x2＜b）都有f（
x1+x2
2
）＞
f(x1)+f(x2)
2
．若S1=\i∈(a，b，)f（x）dx，S2=
f(a)+f(b)
2
（b-a），S3=f（a）（b-a），则S1、S2、S3的大小关系为
 
．
（2012•湖北模拟）设Sn是等比数列{an}的前n项和，若S1，2S2，3S3成等差数列，则公比q等于
1
3
1
3
．
已知等差数列{an}的前n项和为Sn且过点P（n，an）和Q（n+2，an+2）（n∈N*） 的直线的斜率是3，若S1=1，则S8=
92
92
．
已知函数y=f（x）是R上的偶函数，且在区间（-∞，0）是单调递增的，若S1=
∫
2
1
x2dx，S2=
∫
2
1
1
x
dx，S3=
∫
2
1
exdx则下列不等式中一定成立的是（　　）
A、f（S1）＜f（S2）＜f（S3）
B、f（S3）＜f（S2）＜f（S1）
C、f（S2）＜f（S1）＜f（S3）
D、f（S3）＜f（S1）＜f（S2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

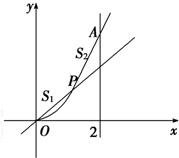精英家教网