【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 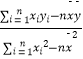 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 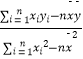 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.