题目内容
【题目】已知a，b是实数，函数f（x）=x|x﹣a|+b．
（1）当a=2时，求函数f（x）的单调区间；
（2）当a＞0时，求函数f（x）在区间[1，2]上的最大值；
（3）若存在a∈[﹣3，0]，使得函数f（x）在[﹣4，5]上恒有三个零点，求b的取值范围．
【答案】
（1）解：当a=2时，f（x）=x|x﹣2|+b= 
，
由二次函数的单调性知，
f（x）在（﹣∞，1]上单调递增，在（1，2）上单调递减，在[2，+∞）上单调递增．
（2）解：设g（x）=x|x﹣a|=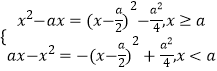 
，ρ
由于a＞0且1≤x≤2，结合函数f（x）的图象可知，
若f（1）=f（2），
即g（1）=g（2），
则|1﹣a|=2|2﹣a|，
平方得1﹣2a+a2=16﹣16a+4a2，
即3a2﹣14a+15=0，
得a=3或a= 
，
当0＜a≤ 时，g（2）≥g（1），此时g（2）最大，即f（2）最大，最大值为f（2）=2|2﹣a|+b=4﹣2a+b，
若 ＜x＜3时，g（2）＜g（1），此时g（1）最大，即f（1）最大，最大值为f（ ）=|1﹣a|+b=1﹣a+b，
若a≥3时，g（2）＞g（1），此时g（2）最大，即f（2）最大，最大值为f（2）=2|2﹣a|+b=2a﹣4+b，
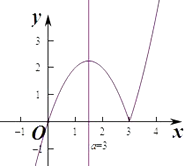
（3）解：若存在a∈[﹣3，0]，使得函数f（x）在[﹣4，5]上恒有三个零点，
则存在a∈[﹣3，0]，使得b=﹣x|x﹣a|有三个不同的实根；
令g（x）=﹣x|x﹣a|= 
，
（ⅰ）当a=0时，g（x）在[﹣4，5]上单调递减，故b无解；
（ⅱ）当﹣3≤a＜0时，g（x）在（﹣∞，a）上单调递减，在[a， 
]上单调递增，在（ ，+∞）上单调递减，
∵g（﹣4）=4|4+a|=16+4a，g（a）=0，g（ ）= 
，g（5）=5a﹣25，
∴g（﹣4）﹣g（ ）= 
＞0，g（a）﹣g（5）=25﹣5a＞0，
∴0＜b＜ ，
∴0＜b＜ 
．
【解析】（1）当a=2时，作出函数f（x）的表达式，利用数形结合即可求函数f（x）的单调区间；（2）当a＞0时，先求出f（1）=f（2），然后利用数形结合即可函数f（x）在区间[1，2]上的最大值；（3）利用参数分离法将条件进行转化，利用数形结合即可求b的取值范围．
