Question

【题目】已知直线l：kx﹣y+1+2k=0（k∈R） （Ⅰ）证明直线l经过定点并求此点的坐标；
（Ⅱ）若直线l不经过第四象限，求k的取值范围；
（Ⅲ）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值及此时直线l的方程．

Answer 1

【答案】解：（I）证明：直线l：kx﹣y+1+2k=0（k∈R），化为：k（x+2）﹣y+1=0，令 ，解得x=﹣2，y=1． ∴直线l经过定点（﹣2，1）．
（Ⅱ）由直线l不经过第四象限，y=kx+2k+1．
则k≥0，
（Ⅲ）直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，
由直线l的方程kx﹣y+1+2k=0可得与坐标轴的交点A ，B（0，1+2k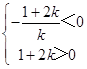）， ，k≠0，解得：k＞0．
∴S= ×|1+2k|= = ≥ 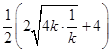=4，当且仅当k= 时取等号．
S的最小值为4，及此时直线l的方程为：x﹣2y+4=0
【解析】（I）直线l：kx﹣y+1+2k=0（k∈R），化为：k（x+2）﹣y+1=0，令 ，解出即可得出．（Ⅱ）由直线l不经过第四象限，y=kx+2k+1．即可得出．（Ⅲ）直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，由直线l的方程kx﹣y+1+2k=0可得与坐标轴的交点A ，B（0，1+2k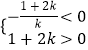）， ，k≠0，解得：k＞0．故S= ×|1+2k|= ，利用基本不等式的性质即可得出．