题目内容
【题目】已知数列![]() 满足对任意的
满足对任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列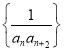 的前
的前![]() 项和为
项和为![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)当n=1,n=2时,直接代入条件![]() 且
且![]() ,可求得;
,可求得;
(2)递推一项,然后做差得![]() ,所以
,所以![]() ;由于
;由于![]() ,即当
,即当![]() 时都有
时都有![]() ,所以数列
,所以数列![]() 是首项为1,公差为1的等差数列,故求得数列
是首项为1,公差为1的等差数列,故求得数列![]() 的通项公式;
的通项公式;
(3)由(2)知![]() ,则
,则![]() ,利用裂项相消法得
,利用裂项相消法得![]() ,根据
,根据![]() 单调递增得
单调递增得![]() ,要使不等式
,要使不等式![]() 对任意正整数n恒成立,只要
对任意正整数n恒成立,只要![]() ,即可求得实数a的取值范围.
,即可求得实数a的取值范围.
试题解析:
(1)解:当![]() 时,有
时,有![]() ,
,
由于![]() ,所以
,所以![]() .
.
当![]() 时,有
时,有![]() ,
,
将![]() 代入上式,由于
代入上式,由于![]() ,所以
,所以![]() .
.
(2)解:由于![]() ,①
,①
则有![]() .②
.②
②-①,得![]() ,
,
由于![]() ,所以
,所以![]() ③
③
同样有![]() ,④
,④
③-④,得![]() .
.
所以![]() .
.
由于![]() ,即当
,即当![]() 时都有
时都有![]() ,
,
所以数列![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
故![]() .
.
(3)解:由(2)知![]() ,则
,则![]() ,所以
,所以

![]() ,∴数列
,∴数列![]() 单调递增 .
单调递增 .
![]() .
.
要使不等式![]() 对任意正整数n恒成立,只要
对任意正整数n恒成立,只要![]() .
.
![]() .
.
![]() ,即
,即![]() .
.
所以,实数a的取值范围是![]() .
.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目