题目内容
【题目】给出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的个数是( )
)(x∈(0,1))其中成立的个数是( )
A.0
B.1
C.2
D.3
【答案】B
【解析】解:对于①,x≥ln(x+1)(x>﹣1),构造函数:f(x)=x﹣ln(x+1)(x>﹣1).f′(x)=1﹣ ![]() =
= ![]() ,可得x∈(﹣1,0),函数f(x)递减,x∈(0,+∞)递增,故f(x)≥f(0)=0 ∴x≥ln(x+1)(x>﹣1)成立,故
,可得x∈(﹣1,0),函数f(x)递减,x∈(0,+∞)递增,故f(x)≥f(0)=0 ∴x≥ln(x+1)(x>﹣1)成立,故 ![]() 成立.
成立.
对于②,取x=1, ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)不成立,故②不成立;
(x>0)不成立,故②不成立;
对于③,ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1)),构造函数g(x)=ln
)(x∈(0,1)),构造函数g(x)=ln ![]() ﹣2(x+
﹣2(x+ ![]() )(x∈(0,1)),
)(x∈(0,1)),
g′(x)= ![]() =
= ![]() 0,∴g(x)在(0,1)递增,而g(0)=0,故x∈(0,1)时,g(x)>0恒成立,故
0,∴g(x)在(0,1)递增,而g(0)=0,故x∈(0,1)时,g(x)>0恒成立,故 ![]() 成立.
成立.
故选:B
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系).

练习册系列答案
相关题目
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 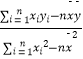 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?