19.若复数z满足($\sqrt{3}$+i)z=4i(i为虚数单位),则复数z的共轭复数为( )
| A. | $\sqrt{3}$+i | B. | $\sqrt{3}$-i | C. | 1+$\sqrt{3}$i | D. | 1-$\sqrt{3}$i |
16. 如图,某几何体的三视图是三个半径为2的圆及其部分,其中半径OA,OB垂直,CD,EF均为直径,则该几何体的体积是( )
如图,某几何体的三视图是三个半径为2的圆及其部分,其中半径OA,OB垂直,CD,EF均为直径,则该几何体的体积是( )
 如图,某几何体的三视图是三个半径为2的圆及其部分,其中半径OA,OB垂直,CD,EF均为直径,则该几何体的体积是( )
如图,某几何体的三视图是三个半径为2的圆及其部分,其中半径OA,OB垂直,CD,EF均为直径,则该几何体的体积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 10π |
15. 已知具有相关关系的两个变量x,y之间的几组数据如下表所示:
已知具有相关关系的两个变量x,y之间的几组数据如下表所示:
(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并估计当x=20时,y的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线2x-y-4=0的右下方的概率.
参考公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
 已知具有相关关系的两个变量x,y之间的几组数据如下表所示:
已知具有相关关系的两个变量x,y之间的几组数据如下表所示:| x | 2 | 4 | 6 | 8 | 10 |
| y | 3 | 6 | 7 | 10 | 12 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并估计当x=20时,y的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线2x-y-4=0的右下方的概率.
参考公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
13. 如图,已知矩形ABCD中,$AB=\frac{4}{3}BC=8$,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥B-ACD,则其外接球的体积为( )
如图,已知矩形ABCD中,$AB=\frac{4}{3}BC=8$,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥B-ACD,则其外接球的体积为( )
0 241433 241441 241447 241451 241457 241459 241463 241469 241471 241477 241483 241487 241489 241493 241499 241501 241507 241511 241513 241517 241519 241523 241525 241527 241528 241529 241531 241532 241533 241535 241537 241541 241543 241547 241549 241553 241559 241561 241567 241571 241573 241577 241583 241589 241591 241597 241601 241603 241609 241613 241619 241627 266669
 如图,已知矩形ABCD中,$AB=\frac{4}{3}BC=8$,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥B-ACD,则其外接球的体积为( )
如图,已知矩形ABCD中,$AB=\frac{4}{3}BC=8$,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥B-ACD,则其外接球的体积为( )| A. | $\frac{500π}{9}$ | B. | $\frac{250π}{3}$ | C. | $\frac{1000π}{3}$ | D. | $\frac{500π}{3}$ |
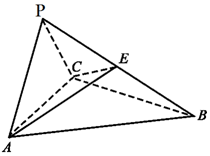 如图,三棱锥P-ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.
如图,三棱锥P-ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.



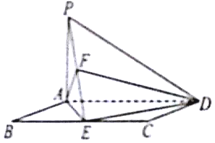 如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.
如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点. 已知多面体ABCDEF中,四边形ABCD为平行四边形,EF⊥CE,且$AC=\sqrt{2}$,AE=EC=1,$EF=\frac{BC}{2}$,AD∥EF.
已知多面体ABCDEF中,四边形ABCD为平行四边形,EF⊥CE,且$AC=\sqrt{2}$,AE=EC=1,$EF=\frac{BC}{2}$,AD∥EF.