题目内容
16．
如图，某几何体的三视图是三个半径为2的圆及其部分，其中半径OA，OB垂直，CD，EF均为直径，则该几何体的体积是（ ）| A． | 4π | B． | 6π | C． | 8π | D． | 10π |
分析 由已知中的三视图，可知该几何体是一个球切去了四分之一，其体积也切去了四分之一，半径代入体积公式乘以四分之三，可得几何体的体积．
解答 解：该几何体直观图如图所示，是一个球的$\frac{3}{4}$，球的半径为2，
∴该几何体的体积$V=\frac{3}{4}×\frac{4}{3}×π×{2^3}=8π$，
故选：C．
点评 本题考查的知识点是由三视图求体积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
6．
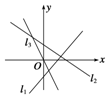如图直线l1，l2，l3的倾斜角分别为α1，α2，α3，则有（ ）
如图直线l1，l2，l3的倾斜角分别为α1，α2，α3，则有（ ）| A． | α1＜α2＜α3 | B． | α1＜α3＜α2 | C． | α3＜α2＜α1 | D． | α2＜α1＜α3 |
11．已知四棱锥P-ABCD的三视图如图所示，则四棱锥P-ABCD的体积是（ ）
| A． | $8\sqrt{5}$ | B． | $\frac{{8\sqrt{5}}}{3}$ | C． | 6 | D． | 8 |