题目内容
15. 已知具有相关关系的两个变量x,y之间的几组数据如下表所示:
已知具有相关关系的两个变量x,y之间的几组数据如下表所示:| x | 2 | 4 | 6 | 8 | 10 |
| y | 3 | 6 | 7 | 10 | 12 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并估计当x=20时,y的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线2x-y-4=0的右下方的概率.
参考公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
分析 (1)根据表中数据画出散点图即可;
(2)计算平均数与回归系数,写出回归直线方程,利用方程计算x=20时y的值;
(3)用列举法求出基本事件数,计算对应的概率值.
解答 解:(1)根据表中数据,画出散点图如图所示: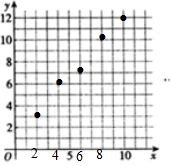
(2)依题意,计算$\overline x=\frac{1}{5}(2+4+6+8+10)=6$,
$\overline y=\frac{1}{5}(3+6+7+10+12)=7.6$,
$\sum_{i=1}^5{x_i^2}=4+16+36+64+100=220$,
$\sum_{i=1}^5{{x_i}{y_i}}=6+24+42+80+120=272$,
b=$\frac{{\sum_{i=1}^5{{x_i}{y_i}-5\overline x\overline y}}}{{\sum_{i=1}^5{x_i^2}-5{{(\overline x)}^2}}}$=$\frac{272-5×6×7.6}{{220-5×{6^2}}}$=$\frac{44}{40}$=1.1,
∴a=7.6-1.1×6=1$;
∴回归直线方程为y=1.1x+1,
当x=20时,y=1.1×20+1=23;
(3)五个点中落在直线2x-y-4=0右下方的三个点记为A,B,C,另外两个点记为d,e,
从这五个点中任取两个点的结果有
(A,B),(A,C),(A,d),(A,e),(B,C),
(B,d),(B,e),(C,d),(C,e),(d,e)共10个,
其中两个点均在直线2x-y-4=0的右下方的结果有3个,
所求的概率为$P=\frac{3}{10}$.
点评 本题考查了散点图与线性回归方程的计算问题,也考查了列举法求古典概型的概率问题,是基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
5.下列几何图形中,可能不是平面图形的是( )
| A. | 梯形 | B. | 菱形 | C. | 平行四边形 | D. | 四边形 |
3.设集合A={1,2,4},B={x|x2+2x+m=0}.若A∩B={1},则B=( )
| A. | {1,-3} | B. | {1,0} | C. | {1,3} | D. | {1,5} |
10.下列说法正确的是( )
| A. | 若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a⊥\overrightarrow b$ | |
| B. | 若a,b,c为实数,且a<b<0,则$\frac{b}{a}<\frac{a}{b}$ | |
| C. | 已知m,n是空间两条不同的直线,α,β,γ是空间三个不同的平面,若α∩γ=m,β∩γ=n,m∥n则α∥β | |
| D. | 已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,若A1B2=A2B1,则l1∥l2 |
7.若角α的顶点为坐标原点,始边在x轴的非负半轴上,终边在直线$y=-\sqrt{3}x$上,则角α的取值集合是( )
| A. | $\{α|α=2kπ-\frac{π}{3},k∈Z\}$ | B. | $\{α|α=2kπ+\frac{2π}{3},k∈Z\}$ | C. | $\{α|α=kπ-\frac{2π}{3},k∈Z\}$ | D. | $\{α|α=kπ-\frac{π}{3},k∈Z\}$ |
4.为了解春季昼夜温差大小与种子发芽多少之间的关系,现从4月的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每50颗种子浸泡后的发芽数,得到如下表格:
(1)从这5天中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于13”的概率;
(2)若4月30日昼夜温差为6/oC,请根据y关于x的线性回归方程$\hat y=\hat bx+\hat a$估计该天种子浸泡后的发芽数.
参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 日期 | 4月1日 | 4月6日 | 4月12日 | 4月19日 | 4月27日 |
| 温差x/oC | 2 | 3 | 5 | 4 | 1 |
| 发芽数y/颗 | 9 | 11 | 15 | 13 | 7 |
(2)若4月30日昼夜温差为6/oC,请根据y关于x的线性回归方程$\hat y=\hat bx+\hat a$估计该天种子浸泡后的发芽数.
参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.



