题目内容
17.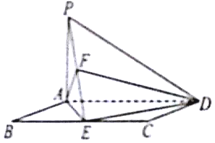 如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.
如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.(Ⅰ)求证:DE⊥平面PAE;
(Ⅱ)若PA=AB=2,F为PE的中点,求三棱锥A-DEF的体积.
分析 (Ⅰ)在矩形ABCD中,由题意可得△ABE,△CDE均为等腰直角三角形,得到AE⊥DE.再由PA⊥平面ABCD,可得PA⊥DE.然后利用线面垂直的判定可得DE⊥平面PAE;
(Ⅱ)直接利用等积法求三棱锥A-DEF的体积.
解答 (Ⅰ)证明:在矩形ABCD中,∵BC=2AB,E为BC的中点.
∴$BE=CE=\frac{1}{2}BC=AB=CD$,
∴△ABE,△CDE均为等腰直角三角形,
∴$∠AEB=∠DEC=\frac{π}{4}$,得AE⊥DE.
∵PA⊥平面ABCD,∴PA⊥DE.
又AE∩PA=A,∴DE⊥平面PAE;
(Ⅱ)解:∵AB=2,∴${S_{△ADE}}=\frac{1}{2}×2×4=4$.
∵F为PE的中点,∴${V_{A-DEF}}={V_{F-ADE}}=\frac{1}{2}{V_{P-ADE}}=\frac{1}{2}×\frac{1}{3}×4×2=\frac{4}{3}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
7.已知函数$f(x)=\sqrt{a{x^2}+ax+3}$的定义域为R,则实数a的取值范围为( )
| A. | $({\frac{1}{3},+∞})$ | B. | (0,12] | C. | [0,12] | D. | $({-∞,\frac{1}{3}}]$ |
5. 阅读如图的程序框图,运行相应的程序,若输入N的值为17,则输出N的值为( )
阅读如图的程序框图,运行相应的程序,若输入N的值为17,则输出N的值为( )
 阅读如图的程序框图,运行相应的程序,若输入N的值为17,则输出N的值为( )
阅读如图的程序框图,运行相应的程序,若输入N的值为17,则输出N的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
12.在△ABC中,若b=8,c=3,A=60°,则此三角形外接圆的半径为( )
| A. | $\frac{{8\sqrt{2}}}{3}$ | B. | $\frac{14}{3}\sqrt{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{{7\sqrt{3}}}{3}$ |
9. 《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )
《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )
 《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )
《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 12立方丈 |
6.若x,y满足$\left\{\begin{array}{l}x+y≥1\\ 2x-y≤0\\ 3x-2y+2≥0\end{array}\right.$则z=3x-y的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
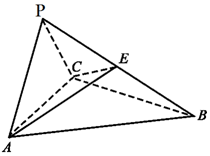 如图,三棱锥P-ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.
如图,三棱锥P-ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.