题目内容
2.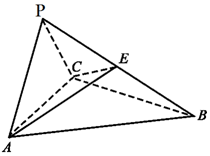 如图,三棱锥P-ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.
如图,三棱锥P-ABC中,△ABC是正三角形,△ACP是直角三角形,∠ABP=∠CBP,AB=BP.(1)证明:平面ACP⊥平面ABC;
(2)若E为棱PB与P不重合的点,且AE⊥CE,求AE与平面ABC所成的角的正弦值.
分析 (1)由已知可得:△ABP≌△CBP.可得AP=CP,由△ACP是直角三角形,可得△ACP是等腰直角三角形,∠APC=90°.取AC的中点O,连接OP,OB.可得OP⊥AC,OB⊥AC.可得OP2+OB2=BP2,可得OP⊥OB.可得OP⊥平面ABC.即可证明结论.
(2)在△ABP中,AE⊥BP,利用面积可得AE=$\frac{\sqrt{7}}{2}$.可得BE=$\frac{3}{2}$.在平面BPO内:过点E作EF⊥OB,垂足为点F,则EF⊥平面ABC,连接AF.可得∠EAF是AE与平面ABC所成的角.进而得出.
解答 (1)证明:∵∠ABP=∠CBP,AB=BP=BC.
∴△ABP≌△CBP.
∴AP=CP,
又△ACP是直角三角形,∴△ACP是等腰直角三角形,∠APC=90°.
Q取AC的中点O,连接OP,OB.
则OP⊥AC,OB⊥AC.
不妨设AC=2.
则OP=1,OB=$\sqrt{3}$,BP=AB=2.
∴OP2+OB2=BP2=4,∴∠BOP=90°.
∴OP⊥OB.又OB∩AC=O.
∴OP⊥平面ABC.OP?平面ACP.
∴平面ACP⊥平面ABC.
(2)解:在△ABP中,AE⊥BP,∴AE=$\frac{\sqrt{2}×\sqrt{{2}^{2}-(\frac{\sqrt{2}}{2})^{2}}}{2}$=$\frac{\sqrt{7}}{2}$.
可得BE=$\sqrt{{2}^{2}-(\frac{\sqrt{7}}{2})^{2}}$=$\frac{3}{2}$.
在平面BPO内:过点E作EF⊥OB,垂足为点F,则EF⊥平面ABC,连接AF.
则∠EAF是AE与平面ABC所成的角.
∴$\frac{EF}{OP}=\frac{BE}{BP}$,可得EF=$\frac{\frac{3}{2}×1}{2}$=$\frac{3}{4}$.
∴sin∠EAF=$\frac{EF}{AE}$=$\frac{3\sqrt{7}}{14}$.
点评 本题考查了空间位置关系、线面面面垂直的判定定理与性质定理、线面角、勾股定理与逆定理,考查了推理能力与计算能力,属于中档题.

| A. | -2 | B. | -$\frac{9}{8}$ | C. | -$\frac{7}{8}$ | D. | 0 |
| A. | 若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a⊥\overrightarrow b$ | |
| B. | 若a,b,c为实数,且a<b<0,则$\frac{b}{a}<\frac{a}{b}$ | |
| C. | 已知m,n是空间两条不同的直线,α,β,γ是空间三个不同的平面,若α∩γ=m,β∩γ=n,m∥n则α∥β | |
| D. | 已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,若A1B2=A2B1,则l1∥l2 |
| A. | $\{α|α=2kπ-\frac{π}{3},k∈Z\}$ | B. | $\{α|α=2kπ+\frac{2π}{3},k∈Z\}$ | C. | $\{α|α=kπ-\frac{2π}{3},k∈Z\}$ | D. | $\{α|α=kπ-\frac{π}{3},k∈Z\}$ |
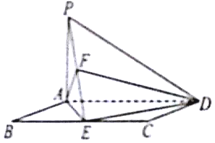 如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.
如图,在矩形ABCD中,BC=2AB,PA⊥平面ABCD,E为BC的中点.