8．如图所示的程序框图表示求算式“2×3×5×9×17×33”之值，则判断框内不能填入（ ）
| A． | k≤33 | B． | k≤38 | C． | k≤50 | D． | k≤65 |
如图，四棱锥P-ABCD中，平面PAC⊥底面ABCD，BC=CD=$\frac{1}{2}$AC=2，∠ACB=∠ACD=$\frac{π}{3}$．
4．
传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏．将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随机从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图．
（Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的2×2列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？
注：K2$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
（Ⅱ）若江西参赛选手共80人，用频率估计概率，试估计其中优秀等级的选手人数；
（Ⅲ）如果在优秀等级的选手中取4名，在良好等级的选手中取2名，再从这6人中任选3人组成一个比赛团队，求所选团队中的有2名选手的等级为优秀的概率．
传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏．将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随机从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图．（Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的2×2列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？
| 优秀 | 合格 | 合计 | |
| 大学组 | |||
| 中学组 | |||
| 合计 |
| P（k2≥k0） | 0.10 | 0.05 | 0.005 |
| k0 | 2.706 | 3.841 | 7.879 |
（Ⅲ）如果在优秀等级的选手中取4名，在良好等级的选手中取2名，再从这6人中任选3人组成一个比赛团队，求所选团队中的有2名选手的等级为优秀的概率．
3．
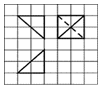如图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥面体的三视图，则该三棱锥的表面积为（ ）
如图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥面体的三视图，则该三棱锥的表面积为（ ）| A． | 2（1+2$\sqrt{2}$+$\sqrt{3}$） | B． | 2（1+$\sqrt{2}$+$\sqrt{3}$） | C． | $4{+}2\sqrt{6}$ | D． | 4（1+$\sqrt{2}$） |
20．在Rt△ABC中，两直角边分别为a，b，斜边为c，则由勾股定理知c2=b2+a2，则在四面体P-ABC中，PA⊥PB，PA⊥PC，PB⊥PC，类比勾股定理，类似的结论为（ ）
0 241401 241409 241415 241419 241425 241427 241431 241437 241439 241445 241451 241455 241457 241461 241467 241469 241475 241479 241481 241485 241487 241491 241493 241495 241496 241497 241499 241500 241501 241503 241505 241509 241511 241515 241517 241521 241527 241529 241535 241539 241541 241545 241551 241557 241559 241565 241569 241571 241577 241581 241587 241595 266669
| A． | S△PBC2=S△PAB2+S△PAC2 | B． | S△ABC2=S△PAB2+S△PAC2 | ||
| C． | S△ABC2=S△PAB2+S△PAC2+S△PBC2 | D． | S△PBC2=S△PAB2+S△PAC2+S△ABC2 |