题目内容
8．如图所示的程序框图表示求算式“2×3×5×9×17×33”之值，则判断框内不能填入（ ）
| A． | k≤33 | B． | k≤38 | C． | k≤50 | D． | k≤65 |
分析 由程序运行的过程看这是一个求几个数的乘积的问题，验算知2×3×5×9×17×33五个数的积故程序只需运行6次．运行6次后，k值变为65，即可得答案．
解答 解：由题设条件可以看出，此程序是一个求几个数的连乘积的问题，
第一次乘入的数是2，由于程序框图表示求算式“2×3×5×9×17×33”之值，
以后所乘的数依次为3，5，9，17，33
2×3×5×9×17×33六个数的积故程序只需运行6次，运行6次后，k值变为65，
当k=33时，应选择“是”，
当k=65时，应选“否”，
所以判断框内不能填入“k≤65”．
故选：D．
点评 本题考查识图的能力，考查根据所给信息给循环结构中判断框填加条件以使程序运行的结果是题目中所给的结果．
练习册系列答案
相关题目
16．如图，在△ABC中，$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{NC}$，P是BN上的一点，若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}$，则实数m的值为（ ）
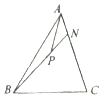
| A． | $\frac{9}{11}$ | B． | $\frac{2}{11}$ | C． | $\frac{3}{11}$ | D． | $\frac{1}{11}$ |
3．
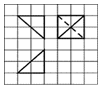如图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥面体的三视图，则该三棱锥的表面积为（ ）
如图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥面体的三视图，则该三棱锥的表面积为（ ）| A． | 2（1+2$\sqrt{2}$+$\sqrt{3}$） | B． | 2（1+$\sqrt{2}$+$\sqrt{3}$） | C． | $4{+}2\sqrt{6}$ | D． | 4（1+$\sqrt{2}$） |
20．已知一组数据3、4、5、s、t的平均数是4，中位数是m，对于任意实数s、t，从3、4、5、s、t、m这组数据中任取一个，取到数字4的概率的最大值为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
18．如果执行如图的框图，则输出的数S=（ ）
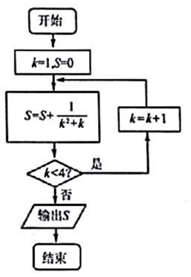
| A． | $\frac{5}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{6}{5}$ | D． | $\frac{5}{6}$ |