题目内容
3.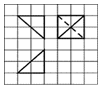 如图所示,网格纸上小正方形的边长为1,粗线画出的是某三棱锥面体的三视图,则该三棱锥的表面积为( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某三棱锥面体的三视图,则该三棱锥的表面积为( )| A. | 2(1+2$\sqrt{2}$+$\sqrt{3}$) | B. | 2(1+$\sqrt{2}$+$\sqrt{3}$) | C. | $4{+}2\sqrt{6}$ | D. | 4(1+$\sqrt{2}$) |
分析 根据三视图知几何体为三棱锥,是棱长为2的正方体一部分,
由正方形的性质求棱长、判断位置关系,由此求出四面体的表面积.
解答 解:根据三视图知几何体为三棱锥P-ABC,是棱长为2的正方体一部分,
直观图如图所示: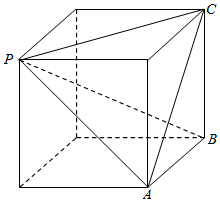
由正方体的性质可得,PC=PA=AC=2$\sqrt{2}$,
PB=2$\sqrt{3}$,
∴BC⊥PC,AB⊥PA,
∴该三棱锥的表面积为:
S=$\frac{1}{2}$×2×2+2×$\frac{1}{2}$×2×2$\sqrt{2}$+$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$×$\frac{\sqrt{3}}{2}$
=2(1+2$\sqrt{2}$+$\sqrt{3}$).
故选:A.
点评 本题考查了由三视图求几何体表面积的应用问题,由三视图借助于正方体复原几何体是解题的关键.

练习册系列答案
相关题目
8.如图所示的程序框图表示求算式“2×3×5×9×17×33”之值,则判断框内不能填入( )


| A. | k≤33 | B. | k≤38 | C. | k≤50 | D. | k≤65 |
15. 我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )
我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )
 我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )
我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )| A. | ①i≤7?②s=s-$\frac{1}{i}$③i=i+1 | B. | ①i≤128?②s=s-$\frac{1}{i}$③i=2i | ||
| C. | ①i≤7?②s=s-$\frac{1}{2i}$③i=i+1 | D. | ①i≤128?②s=s-$\frac{1}{2i}$③i=2i |
12.已知f(x)是定义在R上的奇函数,且当x∈(-∞,0)时,不等式f(x)+xf′(x)<0成立,若a=πf(π),b=(-2)f(-2),c=f(1),则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
