14.在△ABC中,角A,B,C是三角形三内角,则“A≤B”是“sin A≤sin B”的( )
| A. | 必要非充分条件 | B. | 非充分非必要条件 | ||
| C. | 充分必要条件 | D. | 充分非必要条件 |
12.集合﹛x∈Z|(x-2)(x2-3)=0﹜用列举法表示为( )
| A. | ﹛2,$\sqrt{3}$,-$\sqrt{3}$﹜ | B. | ﹛2,$\sqrt{3}$,﹜ | C. | ﹛2,-$\sqrt{3}$﹜ | D. | ﹛2﹜ |
11.为了参加全运会,对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如表.
(1)画出茎叶图
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、标准差,并判断说明选谁参加比赛更合适.
(1)画出茎叶图
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
10.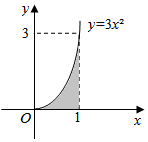 从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
 从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
9.《九章算术》中“开立圆术”曰:“置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径”.“开立圆术”相当于给出了已知球的体积V,求其直径d,公式为$d=\root{3}{{\frac{16}{9}V}}$.如果球的半径为$\frac{1}{3}$,根据“开立圆术”的方法求球的体积为( )
| A. | $\frac{4π}{81}$ | B. | $\frac{π}{6}$ | C. | $\frac{4}{81}$ | D. | $\frac{1}{6}$ |
8.已知f(n)=in-i-n(i为虚数单位,n∈N),函数f(n)的值域的元素个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 无数个 |
7.集合{x∈Z|(x-2)(x2-3)=0}用列举法表示为( )
0 241204 241212 241218 241222 241228 241230 241234 241240 241242 241248 241254 241258 241260 241264 241270 241272 241278 241282 241284 241288 241290 241294 241296 241298 241299 241300 241302 241303 241304 241306 241308 241312 241314 241318 241320 241324 241330 241332 241338 241342 241344 241348 241354 241360 241362 241368 241372 241374 241380 241384 241390 241398 266669
| A. | {2,$\sqrt{3}$,-$\sqrt{3}$} | B. | {2,$\sqrt{3}$} | C. | {2,-$\sqrt{3}$} | D. | {2} |
 如图,半径为1的扇形AOB的圆心角为120°,点C在$\widehat{AB}$上,且∠COA=30°,若$\overrightarrow{OC}$=$λ\overrightarrow{OA}$$+μ\overrightarrow{OB}$,则λ+μ$\sqrt{3}$.
如图,半径为1的扇形AOB的圆心角为120°,点C在$\widehat{AB}$上,且∠COA=30°,若$\overrightarrow{OC}$=$λ\overrightarrow{OA}$$+μ\overrightarrow{OB}$,则λ+μ$\sqrt{3}$.