题目内容
10.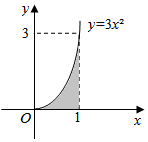 从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )
从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 由题意,分别求出长方形和阴影部分的面积,利用几何概型的公式得到所求.
解答 解:由题意,长方形的面积为3,
阴影部分的面积为${∫}_{0}^{1}3{x}^{2}dx={x}^{3}{|}_{0}^{1}$=1,
由几何概型的公式得到所求概率为$\frac{1}{3}$;
故选C.
点评 本题考查了几何概型的概率求法;关键是明确几何测度为图形面积.

练习册系列答案
相关题目
19.计算${∫}_{0}^{1}$(ex+1)dx=( )
| A. | 2e | B. | e+1 | C. | e | D. | e-1 |
16.已知i是虚数单位,复数z满足z-zi=i,则z的共轭复数$\overline z$=( )
| A. | $\frac{1}{2}+\frac{1}{2}$i | B. | -1-i | C. | -$\frac{1}{2}-\frac{1}{2}$i | D. | 1+i |
 如图,半径为1的扇形AOB的圆心角为120°,点C在$\widehat{AB}$上,且∠COA=30°,若$\overrightarrow{OC}$=$λ\overrightarrow{OA}$$+μ\overrightarrow{OB}$,则λ+μ$\sqrt{3}$.
如图,半径为1的扇形AOB的圆心角为120°,点C在$\widehat{AB}$上,且∠COA=30°,若$\overrightarrow{OC}$=$λ\overrightarrow{OA}$$+μ\overrightarrow{OB}$,则λ+μ$\sqrt{3}$.