9.已知数列{an}的前n项和为${S}_{n}={n}^{2}$,则a5=( )
| A. | 5 | B. | 9 | C. | 16 | D. | 25 |
7.若实数x,y满足x2<y2,则下列不等式成立的是( )
| A. | x<y | B. | -x<y | C. | $\frac{1}{x}$<$\frac{1}{y}$ | D. | |x|<|y| |
6.若球的表面积为16π,则球的体积为( )
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{128π}{3}$ |
5.设α,β是两个不同的平面,m,n,l 是三条不同的直线,下列命题中正确的是( )
| A. | 若α∩β=l,m?α,n?β,则m,n一定相交 | B. | 若α∥β,m?α,n?β,则m,n一定平行 | ||
| C. | 若α∥β,m∥α,n∥β,则m,n一定平行 | D. | 若α⊥β,m⊥α,n⊥β,则m,n一定垂直 |
1.若直线l的方向向量为$\overrightarrow{a}=(1,0,2)$,平面α的法向量为$\overrightarrow{n}$=(-2,0,-4),则( )
| A. | l∥α | B. | l⊥α | C. | l?α | D. | l与α斜交 |
20.为了研究某种细菌在特定条件下随时间变化的繁殖情况,得到如表所示实验数据,若t与y线性相关.
(1)求y关于t的回归直线方程;
(2)预测t=8时细菌繁殖的个数.
(参考公式:$b=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$,$\widehat{y}=\widehat{b}x+\widehat{a}$)
0 241049 241057 241063 241067 241073 241075 241079 241085 241087 241093 241099 241103 241105 241109 241115 241117 241123 241127 241129 241133 241135 241139 241141 241143 241144 241145 241147 241148 241149 241151 241153 241157 241159 241163 241165 241169 241175 241177 241183 241187 241189 241193 241199 241205 241207 241213 241217 241219 241225 241229 241235 241243 266669
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 5 | 6 | 8 | 9 | 12 |
(2)预测t=8时细菌繁殖的个数.
(参考公式:$b=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$,$\widehat{y}=\widehat{b}x+\widehat{a}$)
 如图所示,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
如图所示,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.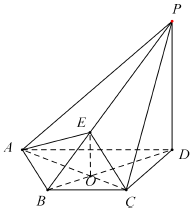 如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.
如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,PA=3,AD=2,AB=4,∠ABC=60°.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,PA=3,AD=2,AB=4,∠ABC=60°.