题目内容
4.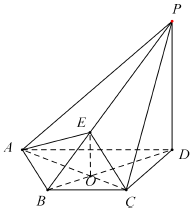 如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.
如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.(1)求证:PD∥平面 AEC;
(2)若BC∥AD,BC=$\sqrt{2}$,AD=2$\sqrt{2}$,PD=3且AB=CD.求三棱锥A-EBC 的体积.
分析 (1)由已知AC⊥BD,BD⊥AE,利用线面垂直的判定可得BD⊥平面AEC,得到BD⊥OE,再由已知PD⊥平面 ABCD,可得PD⊥BD,则PD∥OE.由线面平行的判定可得PD∥平面AEC;
(2)由已知BC∥AD,BC=$\sqrt{2}$,AD=2$\sqrt{2}$,AB=CD,可得四边形ABCD为等腰梯形,结合AC⊥BD求得AO=2OC=2,求出三角形ABC的面积,由(1)知OE为三棱锥E-ABC的高,求出OE,代入棱锥体积公式得答案.
解答 (1)证明:如图,
∵AC⊥BD,BD⊥AE,且AC∩AE=A,
∴BD⊥平面AEC,则BD⊥OE,
又PD⊥平面 ABCD,
∴PD⊥BD,则PD∥OE.
∵OE?平面AEC,PD?平面AEC,
∴PD∥平面AEC;
(2)解:∵BC∥AD,BC=$\sqrt{2}$,AD=2$\sqrt{2}$,AB=CD.
∴四边形ABCD为等腰梯形,
又AC⊥BD,可得AO=2OC=2,∴AC=3.
则${S}_{△ABC}=\frac{1}{2}×3×1=\frac{3}{2}$.
由(1)知OE⊥平面ABC,OE=$\frac{1}{3}PD$,而PD=3,
∴OE=1.
∴${V}_{A-EBC}={V}_{E-ABC}=\frac{1}{3}×\frac{3}{2}×1=\frac{1}{2}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
15.在△ABC中,a,b,c分别为内角的对边,若a=$\sqrt{3}$,A=$\frac{π}{3}$,b=$\sqrt{2}$,则B=( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
12.有关线性回归的说法,不正确的是( )
| A. | 相关关系的两个变量不是因果关系 | |
| B. | 散点图能直观地反映数据的相关程度 | |
| C. | 回归直线最能代表线性相关的两个变量之间的关系 | |
| D. | 任一组数据都有回归方程 |
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右支上非顶点的一点A关于原点O的对称点为B,F为其右焦点,若$\overrightarrow{AF}$•$\overrightarrow{BF}$=0,设∠BAF=θ,且θ∈($\frac{π}{4}$,$\frac{5π}{12}$),则双曲线C离心率的取值范围是( )
| A. | ($\sqrt{2}$,2] | B. | [$\sqrt{2}$,+∞) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
9.已知数列{an}的前n项和为${S}_{n}={n}^{2}$,则a5=( )
| A. | 5 | B. | 9 | C. | 16 | D. | 25 |
 设椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,中心为O,若椭圆过点P(-$\frac{1}{2}$,$\frac{1}{2}$),且AP⊥PO.
设椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,中心为O,若椭圆过点P(-$\frac{1}{2}$,$\frac{1}{2}$),且AP⊥PO. 为了解学生身高情况,某校以8%的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为1:1,测得男生身高情况的频率分布直方图(如图所示):
为了解学生身高情况,某校以8%的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为1:1,测得男生身高情况的频率分布直方图(如图所示):