14.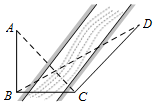 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )| A. | 10米 | B. | $10\sqrt{2}$米 | C. | $10\sqrt{3}$米 | D. | $20\sqrt{3}$米 |
12.要得到函数y=sin2x的图象,只需将函数y=cos2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
11.已知a,b,c,d是四条不同的直线,且a,b是异面直线,则下面说法正确的是( )
| A. | 若c,d 与a,b都相交,则c,d是异面直线 | |
| B. | 若c∥a,d∥b,则 c,d 是异面直线 | |
| C. | 若c,d 与 a,b 都异面,则 c,d 是异面直线 | |
| D. | 若c,d 与 a,b 都垂直,则 c∥d |
10.在三棱柱ABC-A′B′C′中,△ABC是正三角形,侧棱AA′⊥底面ABC,若该三棱柱各棱长相等,则直线A′C与平面BCC′B′所成角的正弦值是( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
9.在△ABC中,AB=2,AC=3,A=60°,则BC=( )
| A. | $\sqrt{6}$ | B. | $\sqrt{7}$ | C. | $\sqrt{19}$ | D. | 2$\sqrt{5}$ |
8.在△ABC中,D是AC边的中点,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,则$\overrightarrow{BD}$=( )
| A. | $\overrightarrow a$-$\frac{1}{2}$$\overrightarrow b$ | B. | $\overrightarrow a$+$\frac{1}{2}$$\overrightarrow b$ | C. | $\frac{1}{2}$$\overrightarrow b$-$\overrightarrow a$ | D. | $\frac{1}{2}$$\overrightarrow b$+$\overrightarrow a$ |
7.如图,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则AO与OE的比值为( )

| A. | $\frac{6}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | 2 |
6.已知函数f(x)=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x,若其图象是由y=sin2x的图象向左平移φ(φ>0)个单位得到的,则φ的最小值为( )
0 240969 240977 240983 240987 240993 240995 240999 241005 241007 241013 241019 241023 241025 241029 241035 241037 241043 241047 241049 241053 241055 241059 241061 241063 241064 241065 241067 241068 241069 241071 241073 241077 241079 241083 241085 241089 241095 241097 241103 241107 241109 241113 241119 241125 241127 241133 241137 241139 241145 241149 241155 241163 266669
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
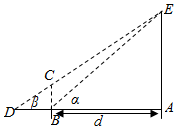 为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题:
为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: 如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥平面ABCD,SD=DC,点E是SC的中点,作EF⊥SB交SB于点F.
如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥平面ABCD,SD=DC,点E是SC的中点,作EF⊥SB交SB于点F.