题目内容
9．在△ABC中，AB=2，AC=3，A=60°，则BC=（ ）| A． | $\sqrt{6}$ | B． | $\sqrt{7}$ | C． | $\sqrt{19}$ | D． | 2$\sqrt{5}$ |
分析 利用余弦定理即可得出．
解答 解：由余弦定理可得：BC2=22+32-2×2×3×cos60°=7，
解得BC=$\sqrt{7}$．
故选：B．
点评 本题考查了余弦定理的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
3．直线$\frac{x}{3}$-$\frac{y}{4}$=1在x轴上的截距是（ ）
| A． | -3 | B． | 3 | C． | -4 | D． | 4 |
20．
如图，在正方体ABCD-A1B1C1D1中，点P在正方体表面运动，如果${S_{△AB{D_1}}}={S_△}_{PB{D_1}}$，那么这样的点P共有（ ）
如图，在正方体ABCD-A1B1C1D1中，点P在正方体表面运动，如果${S_{△AB{D_1}}}={S_△}_{PB{D_1}}$，那么这样的点P共有（ ）| A． | 2个 | B． | 4个 | C． | 6个 | D． | 无数个 |
17．已知m∈N*，则乘积m（m+1）（m+2）…（m+15）可表示为（ ）
| A． | A${\;}_{m}^{15}$ | B． | A${\;}_{m}^{16}$ | C． | A${\;}_{m+15}^{15}$ | D． | A${\;}_{m+15}^{16}$ |
4．复数1-$\frac{i}{3+i}$等于（ ）
| A． | $\frac{9}{10}$-$\frac{3}{10}$i | B． | $\frac{1}{10}$+$\frac{3}{10}$i | C． | $\frac{9}{10}$+$\frac{3}{10}$i | D． | $\frac{1}{10}$-$\frac{3}{10}$i |
14．
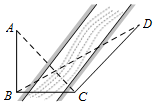如图，某人为测量河对岸塔AB的高，先在塔底B的正东方向上的河岸上选一点C，在点C处测得点A的仰角为45°，并在点C北偏东15°方向的河岸上选定一点D，测得CD的距离为20米，∠BDC=30°，则塔AB的高是（ ）
如图，某人为测量河对岸塔AB的高，先在塔底B的正东方向上的河岸上选一点C，在点C处测得点A的仰角为45°，并在点C北偏东15°方向的河岸上选定一点D，测得CD的距离为20米，∠BDC=30°，则塔AB的高是（ ）| A． | 10米 | B． | $10\sqrt{2}$米 | C． | $10\sqrt{3}$米 | D． | $20\sqrt{3}$米 |
如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$和圆O：x2+y2=b2（其中圆心O为原点），过椭圆C上异于上、下顶点的一点P（x0，y0）引圆O的两条切线，切点分别为A，B．
1．设函数f（x）=ex（3x-1）-ax+a，其中a＜1，若仅有两个整数x0，使得f（x0）＜0，则a的取值范围是（ ）
| A． | [-$\frac{2}{e}$，1] | B． | [$\frac{7}{3{e}^{2}}$，1] | C． | [0，$\frac{2}{e}$] | D． | [$\frac{7}{3{e}^{2}}$，$\frac{2}{e}$] |
如图，平行四边形ABCD的两条对角线相交于点M，点N为CD的中点．若$\overrightarrow{AB}$=（4，0），$\overrightarrow{AD}=（4，4）$．