15.某媒体对“男女同龄退休”这一公众关注的问题进行了民意调查,表是在某单位得到的数据(人数).
(I )能否有90%以上的把握认为对这一问题的看法与性别有关?
(II)从反对“男女同龄退休”的甲、乙等6名男士中选出2人进行陈述,求甲、乙至少有一人被选出的概率.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 赞成 | 反对 | 合计 | |
| 男 | 5 | 6 | 11 |
| 女 | 11 | 3 | 14 |
| 合计 | 16 | 9 | 25 |
(II)从反对“男女同龄退休”的甲、乙等6名男士中选出2人进行陈述,求甲、乙至少有一人被选出的概率.
附:
| P(K2≥k) | 0.25 | 0.15 | 0.10 |
| k | 1.323 | 2.072 | 2.706 |
10.若P(A)=$\frac{3}{4}$,P(B|A)=$\frac{1}{2}$,则P(AB)等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{8}$ |
9.某同学逛书店,发现四本喜欢的书,决定至少买其中的一本,则购买方案有( )
| A. | 4种 | B. | 6种 | C. | 8种 | D. | 15种 |
7.若$tan({\frac{π}{4}-α})=3$,则tanα等于( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
6.满足不等式$\frac{{A}_{n}^{7}}{{A}_{n}^{5}}$>12的n的最小值为( )
0 240007 240015 240021 240025 240031 240033 240037 240043 240045 240051 240057 240061 240063 240067 240073 240075 240081 240085 240087 240091 240093 240097 240099 240101 240102 240103 240105 240106 240107 240109 240111 240115 240117 240121 240123 240127 240133 240135 240141 240145 240147 240151 240157 240163 240165 240171 240175 240177 240183 240187 240193 240201 266669
| A. | 12 | B. | 10 | C. | 9 | D. | 8 |
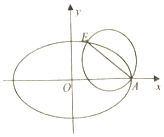 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.