3.“孝敬父母,感恩社会”是中华民族的传统美德,从出生开始,父母就对我们关心无微不至,其中对我们物质帮助是最重要的一个指标,下表是一个统计员在统计《父母为我花了多少》当中使用处理得到下列的数据:
参考数据公式:$\sum_{i=1}^{6}$xiyi=1024.6,$\sum_{i=1}^{6}$xi2=730,$\overline{x}$=9,$\overline{y}$=$\frac{379}{30}$
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$
假设花费累积y与岁数x符合线性相关关系,求:
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利总),那么你每月要偿还父母约多少元钱?
参考数据公式:$\sum_{i=1}^{6}$xiyi=1024.6,$\sum_{i=1}^{6}$xi2=730,$\overline{x}$=9,$\overline{y}$=$\frac{379}{30}$
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利总),那么你每月要偿还父母约多少元钱?
20.已知函数f(x)=cos($\frac{2π}{3}$x)+(a-1)sin($\frac{π}{3}$x)+a,g(x)=2x-x2,若f[g(x)]≤0对x∈[0,1]恒成立,则实数a的取值范围是( )(参考公式:cos(2α)=cos2α-sin2α=2cos2α-1=1-2sin2α)
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
16. 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
0 239952 239960 239966 239970 239976 239978 239982 239988 239990 239996 240002 240006 240008 240012 240018 240020 240026 240030 240032 240036 240038 240042 240044 240046 240047 240048 240050 240051 240052 240054 240056 240060 240062 240066 240068 240072 240078 240080 240086 240090 240092 240096 240102 240108 240110 240116 240120 240122 240128 240132 240138 240146 266669
 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
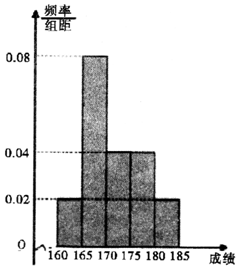 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示: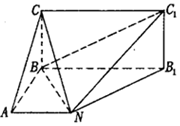 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.