题目内容
20.已知函数f(x)=cos($\frac{2π}{3}$x)+(a-1)sin($\frac{π}{3}$x)+a,g(x)=2x-x2,若f[g(x)]≤0对x∈[0,1]恒成立,则实数a的取值范围是( )(参考公式:cos(2α)=cos2α-sin2α=2cos2α-1=1-2sin2α)| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
分析 在同一坐标系内画出函数$y={x}^{2}+1,y={2}^{x},y={x}^{2}+\frac{3}{2}$的图象,可得$1≤{2}^{x}-{x}^{2}<\frac{3}{2}$,换元后分离参数a,求出函数值域得答案.
解答 解:在同一坐标系内画出函数$y={x}^{2}+1,y={2}^{x},y={x}^{2}+\frac{3}{2}$的图象如图: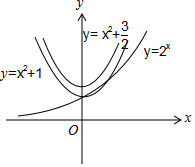
由图可知,在x∈[0,1]上,${x}^{2}+1≤{2}^{x}<{x}^{2}+\frac{3}{2}$恒成立,
即$1≤{2}^{x}-{x}^{2}<\frac{3}{2}$,当且仅当x=0或x=1时等号成立.
∴1≤g(x)<$\frac{3}{2}$.设g(x)=t,则1$≤t<\frac{3}{2}$.
f[g(x)]≤0等价于f(t)≤0,
即cos($\frac{2π}{3}$t)+(a-1)sin($\frac{π}{3}$t)+a≤0,
∵1$≤t<\frac{3}{2}$,∴$\frac{π}{3}t$∈[$\frac{π}{3},\frac{π}{2}$),
再设sin$\frac{π}{3}t$=m,则$\frac{\sqrt{3}}{2}≤m<1$,
则原不等式可化为$1-2si{n}^{2}\frac{π}{3}t+(a-1)sin\frac{π}{3}t+a≤0$,
即1-2m2+(a-1)m+a≤0,
∴a$≤\frac{2{m}^{2}+m-1}{m+1}=2m-1$.
而$\sqrt{3}-1≤2m<1$,∴a$≤\sqrt{3}-1$.
故选:A.
点评 本题考查恒成立问题,考查三角函数的图象和性质,体现了数形结合的解题思想方法,属难题.

练习册系列答案
相关题目
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,-1),|$\overrightarrow{b}$|=1,且$\overrightarrow{b}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
12.复平面上平行四边形ABCD的四个顶点中,A、B、C所对应的复数分别为2-3i、-2-3i、-3+2i,则D点对应的复数是( )
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
9.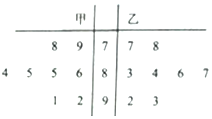 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
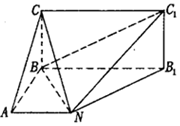 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.