8.设函数f(x)=$\left\{\begin{array}{l}{-|lnx|,x>0}\\{{x}^{2}+2x-1,x≤0}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e-1-2,e2+e-2-2)真假的判断,正确的是( )
| A. | p假q真 | B. | p假q假 | C. | p真q真 | D. | p真q假 |
7.某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
| A. | 20种 | B. | 15种 | C. | 10种 | D. | 4种 |
6.设x>0,由不等式x+$\frac{1}{x}$≥2,x+$\frac{4}{{x}^{2}}$≥3,x+$\frac{27}{{x}^{3}}$≥4,…,推广到x+$\frac{a}{{x}^{n}}$≥n+1,则a=( )
| A. | 2n | B. | 2n | C. | n2 | D. | nn |
5.命题“若a>b,则ac>bc”的逆否命题是( )
| A. | 若a>b,则ac≤bc | B. | 若ac≤bc,则a≤b | C. | 若ac>bc,则a>b | D. | 若a≤b,则ac≤bc |
4.若i为虚数单位,a,b∈R,且$\frac{a+2i}{I}$=b+i,则复数a+bi的模等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
1.设椭圆$\frac{{x}^{2}}{10}$+y2=1和双曲线$\frac{{x}^{2}}{8}$-y2=1的公共焦点分别为F1,F2,P是这两曲线的交点,则△PF1F2的外接圆半径为( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
20.已知抛物线C:y2=2px(p>0)的交点为F,准线为l,过点F的直线与抛物线交于M,N两点,若MR⊥l,垂足为R,且∠NRM=∠NMR,则直线MN的斜率为( )
0 239938 239946 239952 239956 239962 239964 239968 239974 239976 239982 239988 239992 239994 239998 240004 240006 240012 240016 240018 240022 240024 240028 240030 240032 240033 240034 240036 240037 240038 240040 240042 240046 240048 240052 240054 240058 240064 240066 240072 240076 240078 240082 240088 240094 240096 240102 240106 240108 240114 240118 240124 240132 266669
| A. | ±8 | B. | ±4 | C. | ±2$\sqrt{2}$ | D. | ±2 |
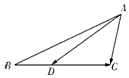 如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.
如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.