题目内容
1.设椭圆$\frac{{x}^{2}}{10}$+y2=1和双曲线$\frac{{x}^{2}}{8}$-y2=1的公共焦点分别为F1,F2,P是这两曲线的交点,则△PF1F2的外接圆半径为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
分析 利用椭圆、双曲线的定义,结合余弦定理,证明PF1⊥PF2,即可求出△PF1F2的外接圆半径.
解答 解:由题意,设P为第一象限的交点,
|PF1|+|PF2|=2$\sqrt{10}$,|PF1|-|PF2|=2$\sqrt{8}$,
∴|PF1|=$\sqrt{10}$+2$\sqrt{2}$,|PF2|=$\sqrt{10}$-2$\sqrt{2}$,
∵|F1F2|=6,
∴cos∠F1PF2=$\frac{20+16-36}{2(10-8)}$=0,
∴PF1⊥PF2,∴F1F2是△PF1F2的外接圆的直径,
则△PF1F2的外接圆半径为3.
故选:D
点评 本题考查椭圆、双曲线的定义,考查余弦定理,利用双曲线和椭圆的定义是解决本题的关键.

练习册系列答案
相关题目
12.在数列1,2,2,3,3,3,4,4,4,4,…中,第31项为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
9.已知一几何体的三视图如图所示,则该几何体的体积为( )
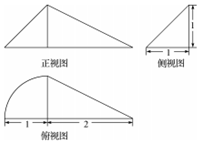

| A. | $\frac{π}{6}+\frac{1}{3}$ | B. | $\frac{π}{12}+1$ | C. | $\frac{π}{12}+\frac{1}{3}$ | D. | $\frac{π}{4}+\frac{1}{3}$ |
6.设x>0,由不等式x+$\frac{1}{x}$≥2,x+$\frac{4}{{x}^{2}}$≥3,x+$\frac{27}{{x}^{3}}$≥4,…,推广到x+$\frac{a}{{x}^{n}}$≥n+1,则a=( )
| A. | 2n | B. | 2n | C. | n2 | D. | nn |
11.某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为$\frac{2}{3}$,C、D两辆汽车每天出车的概率均为$\frac{1}{2}$,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
| 工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
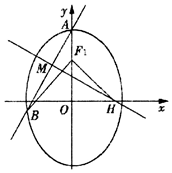 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.