16.在2016年高考结束后,针对高考成绩是否达到了考生自己预期水平的情况,某校在高三部分毕业生内部进行了抽样调查,现从高三年级A、B、C、D、E、F六个班随机抽取了50人,将统计结果制成了如下的表格:
(Ⅰ)根据上述表格的数据估计,该校这些班中,哪个班的学生高考成绩达到自己的预期水平的概率较高?
(Ⅱ)若从A班、F班,从抽查到的达到预期水平的所有对象中,再随机选取2名同学进行详细调查,求选取的2人中含有A班同学的概率.
| 班级 | A | B | C | D | E | F |
| 抽取人数 | 6 | 10 | 12 | 12 | 6 | 4 |
| 其中达到预期水平的人数 | 3 | 6 | 6 | 6 | 4 | 3 |
(Ⅱ)若从A班、F班,从抽查到的达到预期水平的所有对象中,再随机选取2名同学进行详细调查,求选取的2人中含有A班同学的概率.
13.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x,}&{x<0}\\{-\frac{1}{x},}&{x>0}\end{array}\right.$的图象上存在不同的两点A、B,使得曲线y=f(x)在这两点处的切线重合,则点A的横坐标的取值范围可能是( )
| A. | (-$\frac{1}{2}$,0) | B. | (-1,-$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,2) |
12.△ABC的三个内角A、B、C,所对的边分别是a、b、c,若a=2,c=2$\sqrt{3}$,tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB,则△ABC的面积S△ABC=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
11.已知函数f(x)为定义在R上的奇函数,当x>0时,f(x)=4x-2x-f(1),则f(-1)的值为( )
| A. | 1 | B. | -1 | C. | e | D. | -e |
10.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=3x+y的最大值是( )
| A. | 6 | B. | 7 | C. | 0 | D. | 3 |
9.已知命题p:?x∈R,log5x≥0,则( )
| A. | ¬p:?x∈R,log5x<0 | B. | ¬p:?x∈R,log5x≤0 | C. | ¬p:?x∈R,log5x≤0 | D. | ¬p:?x∈R,log5x<0 |
8.设A(1,1)、B(7,4),点C满足$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则点C的坐标是( )
0 239881 239889 239895 239899 239905 239907 239911 239917 239919 239925 239931 239935 239937 239941 239947 239949 239955 239959 239961 239965 239967 239971 239973 239975 239976 239977 239979 239980 239981 239983 239985 239989 239991 239995 239997 240001 240007 240009 240015 240019 240021 240025 240031 240037 240039 240045 240049 240051 240057 240061 240067 240075 266669
| A. | (3,2) | B. | (3,5) | C. | (5,3) | D. | (8,5) |
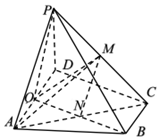 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.