10.设F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,O为坐标原点,若OF的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为$\frac{2}{3}$|OF|,则双曲线的离心率为( )
| A. | $2\sqrt{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $2\sqrt{5}$ | D. | 5 |
8.已知命题p,q,“¬p为假”是“p∨q为真”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.设全集U=R,集合A={y|y=3-x2},B={x|y=log2(x+2)},则(∁UA)∩B=( )
| A. | {x|-2<x≤3} | B. | {x|x>3} | C. | {x|x≥3} | D. | {x|x<-2} |
3. 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),
直到结束为止,则输出的s=( )
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),直到结束为止,则输出的s=( )
| A. | 9 | B. | 27 | C. | 32 | D. | 103 |
2.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的渐近线为等边三角形OAB的边OA、OB所在直线,直线AB过焦点,且|AB|=2,则双曲线实轴长为( )
0 239849 239857 239863 239867 239873 239875 239879 239885 239887 239893 239899 239903 239905 239909 239915 239917 239923 239927 239929 239933 239935 239939 239941 239943 239944 239945 239947 239948 239949 239951 239953 239957 239959 239963 239965 239969 239975 239977 239983 239987 239989 239993 239999 240005 240007 240013 240017 240019 240025 240029 240035 240043 266669
| A. | $\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
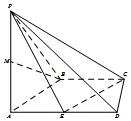 如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.
如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.