题目内容
2.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的渐近线为等边三角形OAB的边OA、OB所在直线,直线AB过焦点,且|AB|=2,则双曲线实轴长为( )| A. | $\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
分析 利用双曲线方程以及渐近线的性质求出a,b关系式,通过|AB|=2,求出c,然后求解a即可得到结果.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的渐近线为等边三角形OAB的边OA、OB所在直线,
可得$\frac{b}{a}=\frac{\sqrt{3}}{3}$,直线AB过焦点,且|AB|=2,
可得c=$\sqrt{3}$,
则$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=\frac{1}{3}$,
解得a=$\frac{3}{2}$.
则双曲线实轴长为:3.
故选:D.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
12.某校开展研究性学习活动需组成指导教师团队,决定用分层抽样的方法从高一、高二、高三三个年级相关教师中抽取,有关数据如下表:(单位:人)
(Ⅰ)求x、y;
(Ⅱ)现要从高二、高三抽取的教师中选取2人作讲座,求这2位教师都来自高三的概率.
| 年级 | 相关教师数 | 抽取教师数 |
| 高一 | x | 4 |
| 高二 | 12 | 2 |
| 高三 | 18 | y |
(Ⅱ)现要从高二、高三抽取的教师中选取2人作讲座,求这2位教师都来自高三的概率.
7.设全集U=R,集合A={y|y=3-x2},B={x|y=log2(x+2)},则(∁UA)∩B=( )
| A. | {x|-2<x≤3} | B. | {x|x>3} | C. | {x|x≥3} | D. | {x|x<-2} |
11.若偶函数f(x)在(-∞,0]上单调递减,a=log2$\frac{1}{3}$,b=log4$\frac{1}{5}$,c=${2^{\frac{3}{2}}}$,则f(a),f(b),f(c)满足( )
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(a)<f(c) | C. | f(c)<f(a)<f(b) | D. | f(c)<f(b)<f(a) |
18.直线l1:ax+y-a+1=0,直线l1:4x+ay-2=0,则“a=±2”是“l1∥l2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
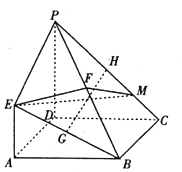 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.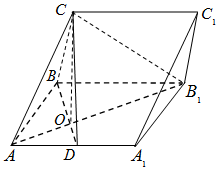 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.