11. 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )| A. | 100πcm3 | B. | $\frac{500π}{3}c{m^3}$ | C. | 400πcm3 | D. | $\frac{4000π}{3}c{m^3}$ |
10. 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
5.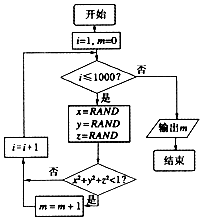 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )| A. | 3.126 | B. | 3.132 | C. | 3.151 | D. | 3.162 |
4.一个几何体的三视图如图所示,该几何体的表面积是$10+2\sqrt{5}$,则图中x的值为( )
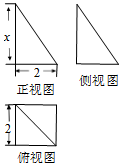

| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
2.我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+$\frac{1}{1+\frac{1}{1+…}}$中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+$\frac{1}{x}$=x求得x=$\frac{\sqrt{5}+1}{2}$.类比上述过程,则$\sqrt{3+2\sqrt{3+2\sqrt{…}}}$=( )
0 239833 239841 239847 239851 239857 239859 239863 239869 239871 239877 239883 239887 239889 239893 239899 239901 239907 239911 239913 239917 239919 239923 239925 239927 239928 239929 239931 239932 239933 239935 239937 239941 239943 239947 239949 239953 239959 239961 239967 239971 239973 239977 239983 239989 239991 239997 240001 240003 240009 240013 240019 240027 266669
| A. | 3 | B. | $\frac{\sqrt{13}+1}{2}$ | C. | 6 | D. | 2$\sqrt{2}$ |
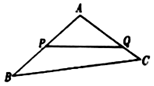 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.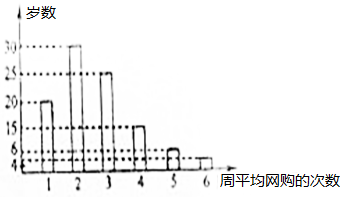 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.