14．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
13．2017年春晚过后，为了研究演员上春晚次数与受关注度的关系，某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计，得到如下数据：
（1）若该演员的粉丝数量g（x）≤g（1）=0与上春晚次数x满足线性回归方程，试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并就此分析，该演员上春晚12次时的粉丝数量；
（2）若用$\frac{{y}_{i}}{{x}_{i}}$（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（四舍五入，精确到整数），从这5个“即时均值”中任选2数，记所选的2数之和为随机变量η，求η的分布列与数学期望．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| 上春晚次数x（单位：次） | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y（单位：万人） | 10 | 20 | 40 | 80 | 100 |
（2）若用$\frac{{y}_{i}}{{x}_{i}}$（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（四舍五入，精确到整数），从这5个“即时均值”中任选2数，记所选的2数之和为随机变量η，求η的分布列与数学期望．
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
12．等比数列{an}的各项均为正数，且a1+2a2=4，a42=4a3a7，则a5=（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{16}$ | C． | 20 | D． | 40 |
5．
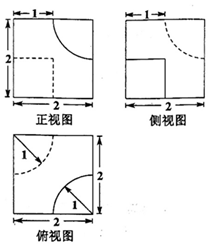如图所示某物体的三视图，则求该物体的体积为（ ）
0 239774 239782 239788 239792 239798 239800 239804 239810 239812 239818 239824 239828 239830 239834 239840 239842 239848 239852 239854 239858 239860 239864 239866 239868 239869 239870 239872 239873 239874 239876 239878 239882 239884 239888 239890 239894 239900 239902 239908 239912 239914 239918 239924 239930 239932 239938 239942 239944 239950 239954 239960 239968 266669
如图所示某物体的三视图，则求该物体的体积为（ ）| A． | $8-\frac{5π}{12}$ | B． | $8-\frac{π}{3}$ | C． | $8-\frac{π}{2}$ | D． | $8-\frac{7π}{12}$ |