16.若$\left\{\begin{array}{l}{sinθ<0}\\{tanθ>0}\end{array}\right.$ 则角θ所在的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
15.要得到函数y=cos(2x+$\frac{π}{3}$)的图象,只需将函数y=cos2x的图象( )
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
13.设z1=3-4i,z2=-2+3i,则z1-z2在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.$\int_0^5{(2x-4)dx}$=( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
11.设z=1-i(为虚数单位),则${z^2}+\frac{2}{z}$=( )
| A. | 1-i | B. | -1+i | C. | -1-i | D. | 1+i |
10.若在甲袋内装有8个白球,4个红球,在乙袋内装有6个白球,6个红球,今从两袋里任意取出1个球,设取出的白球个数为ξ,则下列概率中等于$\frac{{C}_{8}^{1}{C}_{6}^{1}+{C}_{4}^{1}{C}_{6}^{1}}{{C}_{12}^{1}{C}_{12}^{1}}$ 的是( )
0 239730 239738 239744 239748 239754 239756 239760 239766 239768 239774 239780 239784 239786 239790 239796 239798 239804 239808 239810 239814 239816 239820 239822 239824 239825 239826 239828 239829 239830 239832 239834 239838 239840 239844 239846 239850 239856 239858 239864 239868 239870 239874 239880 239886 239888 239894 239898 239900 239906 239910 239916 239924 266669
| A. | P(ξ=0) | B. | P(ξ≤2) | C. | P(ξ=1) | D. | P(ξ=2) |
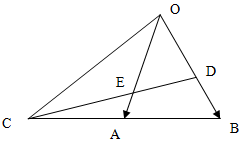 已知△ABO中,延长BA到C,使AC=BA,D是将$\overrightarrow{OB}$分成2:1的一个分点,DC和OA交于E,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$
已知△ABO中,延长BA到C,使AC=BA,D是将$\overrightarrow{OB}$分成2:1的一个分点,DC和OA交于E,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$