题目内容
18.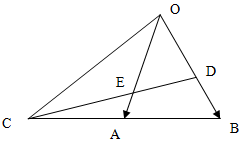 已知△ABO中,延长BA到C,使AC=BA,D是将$\overrightarrow{OB}$分成2:1的一个分点,DC和OA交于E,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$
已知△ABO中,延长BA到C,使AC=BA,D是将$\overrightarrow{OB}$分成2:1的一个分点,DC和OA交于E,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$(1)用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{OC}$,$\overrightarrow{DC}$.
(2)若$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,求实数λ的值.
分析 (1)根据平行四边形的法则结合向量的基本定理即可用用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{OC}$,$\overrightarrow{DC}$.
(2)根据向量关系的条件建立方程关系,求实数λ的值.
解答 解:(1)由题意知A是BC的中点,且$\overrightarrow{OD}$=$\frac{2}{3}$$\overrightarrow{OB}$,
由平行四边形法则得$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OA}$,
则$\overrightarrow{OC}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$=2$\overrightarrow{a}$-$\overrightarrow{b}$,
则$\overrightarrow{DC}$=$\overrightarrow{OC}$-$\overrightarrow{OD}$=2$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{b}$=2$\overrightarrow{a}$-$\frac{5}{3}$$\overrightarrow{b}$;
(2)由图知$\overrightarrow{EC}$∥$\overrightarrow{DC}$,
∵$\overrightarrow{EC}$=$\overrightarrow{OC}$-$\overrightarrow{OE}$=2$\overrightarrow{a}$-$\overrightarrow{b}$-λ$\overrightarrow{a}$=(2-λ)$\overrightarrow{a}$-$\overrightarrow{b}$,
$\overrightarrow{DC}$=2$\overrightarrow{a}$-$\frac{5}{3}$$\overrightarrow{b}$,
∴$\frac{2-λ}{2}$=$\frac{-1}{-\frac{5}{3}}$,解得λ=$\frac{4}{5}$.
点评 本题主要考查向量的基本定理的应用,根据向量平行四边形法则和向量共线的条件是解决本题的关键.

| A. | 6 | B. | 12 | C. | 16 | D. | 24 |
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |