题目内容
9.已知数列{an}是等差数列,且$\left\{{{2^{a_n}}}\right\}$的第3项为8,第5项为128.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,求数列的前n项和Tn.
分析 (1)由${2}^{{a}_{3}}$=8,$,{2}^{{a}_{5}}$=128,可得a3=3,a5=7,再利用等差数列的通项公式及其性质即可得出.
(2)${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n-3)(2n-1)}=\frac{1}{2}(\frac{1}{2n-3}-\frac{1}{2n-1})$,利用裂项求和方法即可得出.
解答 解:(1)由${2}^{{a}_{3}}$=8,$,{2}^{{a}_{5}}$=128,可得a3=3,a5=7,
设数列{an}的公差为d,则2d=a5-a3=4⇒d=2,
所以an=a3+(n-3)d=2n-3.
(2)因为${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n-3)(2n-1)}=\frac{1}{2}(\frac{1}{2n-3}-\frac{1}{2n-1})$,
所以Tn=$\frac{1}{2}[(-1-1)$+$(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-3}-\frac{1}{2n-1})]$=$\frac{1}{2}(-1-\frac{1}{2n-1})$=$\frac{n}{1-2n}$.
点评 本题考查了等差数列的通项公式与求和公式、裂项求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.在△ABC中,$\overrightarrow{AB}⊥\overrightarrow{AC}$,$\overrightarrow{AB}=(1,-2)$,$\overrightarrow{AC}=(4,λ)$,则λ=( )
| A. | -2 | B. | 2 | C. | 8 | D. | -8 |
17.等差数列{an}中,a2=1,a5=6,则公差d等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{3}$ |
4.已知数列{an}中,a1=1,an+1=an+n+1,则数列$\{\frac{a_n}{n}\}$的前n项和为( )
| A. | $\frac{{{n^2}+5n}}{2}$ | B. | $\frac{{{n^2}+5n}}{4}$ | C. | $\frac{{{n^2}+3n}}{2}$ | D. | $\frac{{{n^2}+3n}}{4}$ |
1.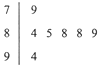 如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )
如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )
 如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )
如图是2015年日喀则市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是( )| A. | 86.5; 86.7 | B. | 88; 86.7 | C. | 88;86.8 | D. | 86.5;86.8 |
18.若$\frac{2+ai}{1+i}$=x+yi(a,x,y∈R),且xy>1,则实数a的取值范围是( )
| A. | (2$\sqrt{2}$,+∞) | B. | (-∞,-2$\sqrt{2}$)∪(2$\sqrt{2}$,+∞) | C. | (-2$\sqrt{2}$,2)∪(2$\sqrt{2}$,+∞) | D. | (-∞,-2)∪(2,+∞) |