$\int 0^5{A．5B．4C．3D．2 题目和参考答案——青夏教育精英家教网——

题目内容

12．$\int_0^5{（2x-4）dx}$=（　　）

A．

5

B．

4

C．

3

D．

2

分析求出被积函数的原函数，然后根据定积分的定义计算

解答解：$\int_0^5{（2x-4）dx}$=（x²-4x）|${\;}_{0}^{5}$=25-20=5，
故选：A

点评本题主要考查了定积分的简单应用，解题的关键是求被积函数的原函数，属于基础题．

练习册系列答案

激活思维优加课堂系列答案

全能达标100分系列答案

智能考核卷系列答案

活力试卷系列答案

琢玉计划系列答案

小学全能测试卷系列答案

名校全优考卷系列答案

课课优能力培优100分系列答案

期末迎考特训系列答案

高效课时100系列答案

相关题目

2．函数f（x）=Asin（ωx+φ）的部分图象如图所示，若f（4）=-f（6）=-1，且$f（\frac{1}{2}）=0$，则f（2017）=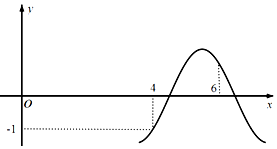

$\frac{\sqrt{2}}{2}$

$\frac{\sqrt{3}}{2}$

3．一个三层书架，分别放置语文书12本，数学书14本，英语书11本，从中取出一本，则不同的取法37种．（以数字作答）

20．设e，f，g，h四个数成递增的等差数列，且公差为d，若eh=13，f+g=14，则d等于（　　）

7．若{log₂a_n}是首项为1，公差为2的等差数列，则数列{na_n}的前n项和为$\frac{2+（6n-2）•{4}^{n}}{9}$．

17．已知△ABC的顶点分别为A（2，1），B（3，2），C（-3，-1），D在直线BC上．
（Ⅰ）若$\overrightarrow{BC}$=2$\overrightarrow{BD}$，求点D的坐标；
（Ⅱ）若AD⊥BC，求点D的坐标．

4．已知数列{a_n}中，a₁=3，且点P_n（a_n，a_n+1）（n∈N^*）在直线4x-y+1=0上，则数列{a_n}的通项公式为a_n=$\frac{10}{3}•{4}^{n-1}$$-\frac{1}{3}$．

1．若$\frac{2+ai}{1+i}$=x+yi（a，x，y均为实数），则x-y=（　　）

2．将函数y=sinxcosx的图象向右平移m（m＞0）个单位，所得曲线的对称轴与函数$y=cos（{ωx+\frac{π}{3}}）（{ω＞0}）$的图象的对称轴重合，则实数m的最小值为$\frac{π}{12}$．