7.过坐标原点O的直线l与圆C:(x+1)2+(y-$\sqrt{3}$)2=100相交于A,B两点,当△ABO的面积最大时,则直线l的斜率是( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
5.△ABC的三个内角A,B,C所对的边分别为a,b,c,若A=45°,B=75°,c=3$\sqrt{2}$,则a=( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
4.若函数f(x)=a3-cosx,则f'(a)=( )
| A. | 3a2+sina | B. | 3a2-sina | C. | sina | D. | cosa |
3.为了对某班学生的数学、物理成绩进行分析,从该班25位男同学,15位女同学中随机抽取一个容量为8的样本.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式,不必计算出结果);
(2)若这8人的数学成绩从小到大排序是65,68,72,79,81,88,92,95.物理成绩从小到大排序是72,77,80,84,86,90,93,98.
①求这8人中恰有3人数学、物理成绩均在85分以上的概率(结果用分数表示);
②已知随机抽取的8人的数学成绩和物理成绩如表:
若以数学成绩为解释变量x,物理成绩为预报变量y,求y关于x的线性回归方程(系数精确到0.01);并求数学成绩对于物理成绩的贡献率R2(精确到0.01).
参考公式:相关系数:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,R2=r2,
回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据:$\overline{x}$=80,$\overline{y}$=85,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2=868,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2═518,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$)=664,$\sqrt{868}$≈29.5,$\sqrt{518}$≈22.8.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式,不必计算出结果);
(2)若这8人的数学成绩从小到大排序是65,68,72,79,81,88,92,95.物理成绩从小到大排序是72,77,80,84,86,90,93,98.
①求这8人中恰有3人数学、物理成绩均在85分以上的概率(结果用分数表示);
②已知随机抽取的8人的数学成绩和物理成绩如表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学成绩 | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| 物理成绩 | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
参考公式:相关系数:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,R2=r2,
回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据:$\overline{x}$=80,$\overline{y}$=85,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2=868,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2═518,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$)=664,$\sqrt{868}$≈29.5,$\sqrt{518}$≈22.8.
2.从一批含有11只正品,2只次品的产品中,不放回地抽取3次,每次抽取1只,设抽得次品数为X,则E(5X+1)的值为( )
| A. | $\frac{42}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{41}{11}$ | D. | $\frac{6}{13}$ |
1.已知四面体P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=$\sqrt{3}$AB,若四面体P-ABC 的体积为$\frac{3}{2}$,求球的表面积( )
| A. | 8π | B. | 12π | C. | 8$\sqrt{3}$π | D. | 12$\sqrt{3}$π |
18.扇形AOB的中心角为2θ,θ∈(0,$\frac{π}{2}$),半径为r,在扇形AOB中作内切圆O1与圆O1外切,与OA,OB相切的圆O2,问sinθ为何值时,圆O2的面积最大?最大值是多少?
0 239535 239543 239549 239553 239559 239561 239565 239571 239573 239579 239585 239589 239591 239595 239601 239603 239609 239613 239615 239619 239621 239625 239627 239629 239630 239631 239633 239634 239635 239637 239639 239643 239645 239649 239651 239655 239661 239663 239669 239673 239675 239679 239685 239691 239693 239699 239703 239705 239711 239715 239721 239729 266669
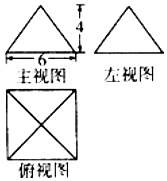 已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.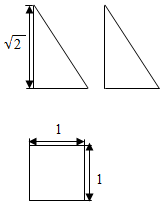 某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.
某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.