题目内容
5.△ABC的三个内角A,B,C所对的边分别为a,b,c,若A=45°,B=75°,c=3$\sqrt{2}$,则a=( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
分析 先根据三角形的内角和定理求出C,再根据正弦定理代值计算即可.
解答 解:∵A=45°,B=75°,
∴C=180°-A-B=120°
由正弦定理可得$\frac{a}{sinA}$=$\frac{c}{sinC}$,
即a=$\frac{csinA}{sinC}$=$\frac{3\sqrt{2}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$,
故选:B.
点评 本题考查了正弦定理的应用,以及学生的运算能力,属于基础题

练习册系列答案
相关题目
16.如果$\frac{x^2}{4}+\frac{y^2}{m}=1$表示焦点在x轴的椭圆,则实数m的取值范围是( )
| A. | (0,4] | B. | (0,4) | C. | (4,+∞) | D. | [4,+∞) |
17.函数$f(x)=\frac{1}{2}{x^2}-lnx$的单调减区间( )
| A. | (-1,1] | B. | (0,1] | C. | (1,+∞) | D. | (0,+∞) |
14.已知复数z1=3-bi,z2=1-2i(i是虚数单位),若$\frac{{z}_{1}}{{z}_{2}}$是纯虚数,则实数b的值为( )
| A. | 3 | B. | -$\frac{3}{2}$ | C. | 6 | D. | -6 |
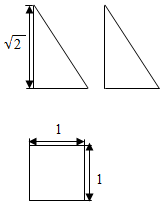 某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.
某几何体的三视图如图所示,设该几何体中最长棱所在的直线为m,与直线m不相交的其中一条棱所在直线为n,则直线m与n所成的角为$\frac{π}{3}$.