��Ŀ����
3��Ϊ�˶�ij��ѧ������ѧ�������ɼ����з������Ӹð�25λ��ͬѧ��15λŮͬѧ�������ȡһ������Ϊ8����������1��������Ա�����ֲ���������Եõ����ٸ���ͬ����������ֻҪ��д����ʽ�����ؼ�����������
��2������8�˵���ѧ�ɼ���С����������65��68��72��79��81��88��92��95�������ɼ���С����������72��77��80��84��86��90��93��98��
������8����ǡ��3����ѧ�������ɼ�����85�����ϵĸ��ʣ�����÷�����ʾ����
����֪�����ȡ��8�˵���ѧ�ɼ��������ɼ������
| ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ��ѧ�ɼ� | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| �����ɼ� | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
�ο���ʽ�����ϵ����r=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sqrt{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}\sum_{i=1}^{n}��{y}_{i}-\overline{y}��^{2}}}$��R2=r2��
�ع鷽�̣�$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$����$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$
�ο����ݣ�$\overline{x}$=80��$\overline{y}$=85��$\sum_{i=1}^{8}$��xi-$\overline{x}$��2=868��$\sum_{i=1}^{8}$��yi-$\overline{y}$��2�T518��$\sum_{i=1}^{8}$��xi-$\overline{x}$����yi-$\overline{y}$��=664��$\sqrt{868}$��29.5��$\sqrt{518}$��22.8��
���� ��1�������������ȡ����Ů�����������������ʽ������ܵ���Ϸ�����
��2���ֲ�������Ϸ������ټ�����ʣ�
��2������������ʽ�����ݽ��м��㣬�ó��ع鷽�̺����ϵ����
��� �⣺��1����25λ��ͬѧ��15λŮͬѧ�������ȡһ������Ϊ8��������
���Ա�����ֲ��������������ȡ8��$\frac{25}{25+15}$=5���ˣ���Ů����ȡ8-5=3���ˣ���
���Եõ���ͬ����������${C}_{25}^{5}$•${C}_{15}^{3}$��
��2������ѧ�ɼ���85�����ϵ���3�ˣ������ɼ���85�����ϵ���4�ˣ�
��һ������������4�����������ѡ3������ѧ���������Ӧ��������A${\;}_{4}^{3}$��
�ڶ�������ʣ�µ�5����ѧ�������������������Ӧ��������${A}_{5}^{5}$�����ݳ˷�ԭ�������������Ĵ���������${A}_{4}^{3}{•A}_{5}^{5}$��
��8λͬѧ��������������ѧ�����ֱ��Ӧ����������${A}_{8}^{8}$�֣�
������ĸ���P=$\frac{{A}_{4}^{3}{•A}_{5}^{5}}{{A}_{8}^{8}}$=$\frac{1}{14}$��
����y��x�����Իع鷽����$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$����$\stackrel{��}{b}$=$\frac{664}{868}$��0.76��$\stackrel{��}{a}$=85-0.76��80��24.2��
����y��x�����Իع鷽����$\stackrel{��}{y}$=0.76x+24.2��
r=$\frac{664}{29.5��22.8}$��0.987��R2=0.9872��0.97��
���� ���⿼���˷ֲ�������������ʽ��Ӧ�ã����Իع鷽�̣������е��⣮

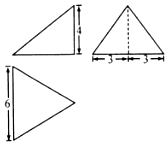 ��ͼ��ij����������ͼ������ͼ����ͼ�ֱ���ֱ�������Ρ����������κ͵ȱ������Σ����������Ķ��㶼��ͬһ�����ϣ������ı����Ϊ��������
��ͼ��ij����������ͼ������ͼ����ͼ�ֱ���ֱ�������Ρ����������κ͵ȱ������Σ����������Ķ��㶼��ͬһ�����ϣ������ı����Ϊ��������| A�� | 27�� | B�� | 48�� | C�� | 64�� | D�� | 81�� |
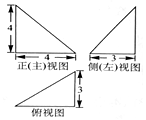 ij����������ͼ��ͼ��ʾ��������������Ϊ��������
ij����������ͼ��ͼ��ʾ��������������Ϊ��������| A�� | 8 | B�� | 10 | C�� | 20 | D�� | 24 |
| A�� | a��b��c | B�� | a��b��c | C�� | b��a��c | D�� | b��a��c |
| A�� | ��-$\frac{1}{2}$��+�ޣ� | B�� | ��$\frac{-3+\sqrt{3}}{2}$��+�ޣ� | C�� | ��$\frac{-3+\sqrt{3}}{2}$��$\frac{1}{2}$�� | D�� | ��0��+�ޣ� |
| A�� | A��B | B�� | sin2A��sin2B | C�� | cos2A��cos2B | D�� | a��b |
