3.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )
| A. | -$\frac{π}{2}$ | B. | 2kπ-$\frac{π}{2}$(k∈Z) | C. | kπ(k∈Z) | D. | kπ+$\frac{π}{2}$(k∈Z) |
2.实数a,b,c不全为0等价于为( )
| A. | a,b,c均不为0 | B. | a,b,c中至多有一个为0 | ||
| C. | a,b,c中至少有一个为0 | D. | a,b,c中至少有一个不为0 |
1.下列四个结论,正确的是( )
①a>b,c<d⇒a-c>b-d
②a>b>0,c<d<0⇒ac>bd
③a>b>0⇒$\root{3}{a}$>$\root{3}{b}$
④a>b>0⇒$\frac{1}{{a}^{2}}$>$\frac{1}{{b}^{2}}$.
0 239475 239483 239489 239493 239499 239501 239505 239511 239513 239519 239525 239529 239531 239535 239541 239543 239549 239553 239555 239559 239561 239565 239567 239569 239570 239571 239573 239574 239575 239577 239579 239583 239585 239589 239591 239595 239601 239603 239609 239613 239615 239619 239625 239631 239633 239639 239643 239645 239651 239655 239661 239669 266669
①a>b,c<d⇒a-c>b-d
②a>b>0,c<d<0⇒ac>bd
③a>b>0⇒$\root{3}{a}$>$\root{3}{b}$
④a>b>0⇒$\frac{1}{{a}^{2}}$>$\frac{1}{{b}^{2}}$.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
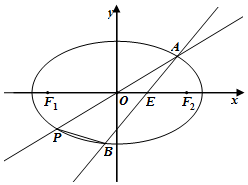 如图,在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{6}}{3}$,a=$\sqrt{6}$,直线l与x轴交于点E,与椭圆C交于A、B两点.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{6}}{3}$,a=$\sqrt{6}$,直线l与x轴交于点E,与椭圆C交于A、B两点.