题目内容

2．实数a，b，c不全为0等价于为（　　）
A．a，b，c均不为0B．a，b，c中至多有一个为0
C．a，b，c中至少有一个为0D．a，b，c中至少有一个不为0

分析 利用充要条件的意义即可得出．

解答 解：实数a，b，c不全为0等价于为a，b，c中至少有一个不为0，
故选：D

点评 本题考查了简易逻辑的有关知识，考查了推理能力，属于基础题．

练习册系列答案
相关题目
12．下列说法中，正确的有③④．（写出所有正确说法的序号）
①已知关于x的不等式mx2+mx+1＞0的解集为R，则实数m的取值范围是0＜m＜4．
②已知等比数列{an}的前n项和为Sn，则Sn、S2n-Sn、S3n-S2n也构成等比数列．
③已知a＞0，b＞-1，且a+b=1，则$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$的最小值为$\frac{3+2\sqrt{2}}{2}$．
④在△DEF中，DE=2，EF=3，∠DEF=60°，M是DF的中点，N在EF上，且DN⊥ME，则$\overrightarrow{DN}$•$\overrightarrow{EF}$=$\frac{9}{4}$．
13．从含有4件正品、2件次品的6件产品中，随机抽取3件，则恰好抽到1件次品的概率（　　）
A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{3}{5}$
10．已知函数f（x）=$\left\{\begin{array}{l}{x}^{2}+（4a-3）x+3a，x＜0\\-sinx，0≤x＜\frac{π}{2}\end{array}\right.$在定义域内为单调递减函数，则a的取值范围为（　　）
A．（0，$\frac{4}{3}$）B．$（0，\left.\frac{4}{3}]$C．$[0，\right.\frac{4}{3}）$D．$[0，\left.\frac{4}{3}]\right.$
17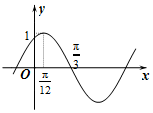．$f（x）=Asin（ωx+φ）（A＞0，|φ|＜\frac{π}{2}）$的图象如图所示，为了得到f（x）的图象，则只要将g（x）=cos2x的图象（　　）
A．向右平移$\frac{π}{12}$个单位长度B．向右平移$\frac{π}{6}$个单位长度
C．向左平移$\frac{π}{12}$个单位长度D．向左平移$\frac{π}{6}$个单位长度
7．曲线y=2lnx在点（e，2）处的切线与y轴交点的坐标为（0，0）．
14．已知$\frac{4+mi}{1+2i}$∈R，且m∈R，则|m+6i|=（　　）
A．6B．8C．8$\sqrt{3}$D．10
11．若输入5，如图中所示程序框图运行后，输出的结果是（　　）
A．1B．0C．-1D．-5
12．数列an=2n+1，其前n项和为Tn，若不等式nlog2（Tn+4）-λ（n+1）+7≥3n对一切n∈N*恒成立，则实数λ的取值范围为（　　）
A．λ≤3B．λ≤4C．2≤λ≤3D．3≤λ≤4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网