题目内容
8.函数f(x)=ax(a>1)与函数g(x)=x2图象有三个不同的公共点,则实数a的取值范围是(1,e${\;}^{\frac{2}{e}}$).分析 x<0时,必有一个交点,x>0时,由ax-x2=0,可得lna=$\frac{2lnx}{x}$,构造函数,确定函数的单调性,根据函数的单调性得出lna的范围即可得出答案.
解答 解:x>0时,由ax-x2=0,可得ax=x2,∴xlna=2lnx,
∴lna=$\frac{2lnx}{x}$,
令h(x)=$\frac{2lnx}{x}$,则h′(x)=$\frac{2-2lnx}{{x}^{2}}$=0,可得x=e,
∴函数在(0,e)上单调增,在(e,+∞)上单调减,
∴h(x)max=h(e)=$\frac{2}{e}$,
∴lna<$\frac{2}{e}$,
∴1<a<e${\;}^{\frac{2}{e}}$
又x<0时,必有一个交点,
∴1<a<e${\;}^{\frac{2}{e}}$时,函数f(x)=ax-x2(a>1)有三个不同的零点,
故答案为:(1,e${\;}^{\frac{2}{e}}$).
点评 本题考查函数的零点,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知曲线y=x3在(a,b)处的切线斜率为3,那么a的值是( )
| A. | -1 | B. | 1 | C. | -1或1 | D. | 2 |
16.$cos\sqrt{2},sin\sqrt{2},tan\sqrt{2}$的大小关系是( )
| A. | $sin\sqrt{2}<cos\sqrt{2}<tan\sqrt{2}$ | B. | $cos\sqrt{2}<sin\sqrt{2}<tan\sqrt{2}$ | C. | $cos\sqrt{2}<tan\sqrt{2}<sin\sqrt{2}$ | D. | $sin\sqrt{2}<tan\sqrt{2}<cos\sqrt{2}$ |
3.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )
| A. | -$\frac{π}{2}$ | B. | 2kπ-$\frac{π}{2}$(k∈Z) | C. | kπ(k∈Z) | D. | kπ+$\frac{π}{2}$(k∈Z) |
17.下面与角$\frac{23π}{3}$终边相同的角是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |

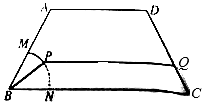 如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.
如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.