9．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$右焦点为F.过F作与x轴垂直的直线l与两条渐近线相交于A.B两点.P是直线l与双曲线的一个交点．设O为坐标原点．若有实——青夏教育精英家教网——

9．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$右焦点为F，过F作与x轴垂直的直线l与两条渐近线相交于A、B两点，P是直线l与双曲线的一个交点．设O为坐标原点．若有实数m、n，使得$\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$，且$mn=\frac{2}{9}$，则该双曲线的离心率为（　　）

$\frac{{3\sqrt{2}}}{4}$

$\frac{{3\sqrt{5}}}{5}$

$\frac{{3\sqrt{2}}}{2}$

执行如图程序框图，若输出y=2，则输入的x为（　　）

-1或$±\sqrt{2}$

7．使奇函数f（x）=sin（2x+θ）+$\sqrt{3}$cos（2x+θ）在[-$\frac{π}{4}$，0]上为减函数的θ（θ∈（0，π））的值为$\frac{2π}{3}$．

6．用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$＜n（n∈N*）过程中，由n=k递推到n=k+1时，不等式左端增加的项数是（　　）

5．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F₁，F₂，过F₂作一条直线（不与x轴垂直）与椭圆交于A，B两点，如果△ABF₁恰好为等腰直角三角形，该直线的斜率为（　　）

4．已知函数f（x）=x²-2x+mlnx（m∈R），$g（x）=（x-\frac{3}{4}）{e^x}$．
（Ⅰ）若m=1，求y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）若f（x）存在两个极值点x₁，x₂（x₁＜x₂），求g（x₁-x₂）的最小值．

3．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），O是坐标原点，F₁，F₂分别为其左右焦点，|F₁F₂|=2$\sqrt{3}$，M是椭圆上一点，∠F₁MF₂的最大值为$\frac{2}{3}$π．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l与椭圆C交于P，Q两点，且OP⊥OQ，
（i）求证：$\frac{1}{{{{|{OP}|}^2}}}+\frac{1}{{{{|{OQ}|}^2}}}$为定值；
（ii）求△OPQ面积的最小值．

2．经国务院批复同意，重庆成功入围国家中心城市，某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分（满分100分），得到如图所示茎叶图：

（Ⅰ）计算女生打分的平均分，并用茎叶图的数字特征评价男生、女生打分谁更分散；
（Ⅱ）如图按照打分区间[0，60）、[60，70）、[70，80）、[80，90）、[90，100]绘制的直方图中，求最高矩形的高h；
（Ⅲ）从打分在70分以下（不含70分）的同学中抽取3人，求有女生被抽中的概率．

1．已知函数f（x）=x²（2^x-2^-x），则不等式f（2x+1）+f（1）＜0的解集是（　　）

$（{-∞，-\frac{1}{2}}）$

（-∞，-1）

$（{-\frac{1}{2}，+∞}）$

（-1，+∞）

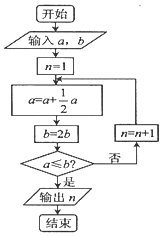宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．如图是源于其思想的一个程序框图，若输入的a，b分别为3，2，则输出的n=（　　）

0 239392 239400 239406 239410 239416 239418 239422 239428 239430 239436 239442 239446 239448 239452 239458 239460 239466 239470 239472 239476 239478 239482 239484 239486 239487 239488 239490 239491 239492 239494 239496 239500 239502 239506 239508 239512 239518 239520 239526 239530 239532 239536 239542 239548 239550 239556 239560 239562 239568 239572 239578 239586 266669