题目内容
5.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )| A. | ±1 | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\sqrt{3}$ |
分析 假设△ABF1构成以A为直角顶点的等腰直角三角形,根据椭圆的定义及性质求得|AF1|=2(2-$\sqrt{2}$)a,|AF2|=2a-m=(2$\sqrt{2}$-2)a,则直线AB的斜率为k=±tan∠AF2F1=±$\sqrt{2}$.
解答  解:可设|F1F2|=2c,|AF1|=m,
解:可设|F1F2|=2c,|AF1|=m,
若△ABF1构成以A为直角顶点的等腰直角三角形,
则|AB|=|AF1|=m,|BF1|=$\sqrt{2}$m,
由椭圆的定义可得△ABF1的周长为4a,
即有4a=2m+$\sqrt{2}$m,即m=2(2-$\sqrt{2}$)a,
∴|AF1|=2(2-$\sqrt{2}$)a,
则|AF2|=2a-m=(2$\sqrt{2}$-2)a,
在Rt△AF1F2中,
tan∠AF2F1=$\frac{丨A{F}_{1}丨}{丨A{F}_{2}丨}$=$\sqrt{2}$,
∴直线AB的斜率为k=±tan∠AF2F1=±$\sqrt{2}$,
故选:C.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线斜率与倾斜角的关系,考查计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
16.设a,b都是不等于1的正数,则“${log_a}^2<{log_b}^2$”是“2a>2b>2”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
13. 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有平面A′GF⊥平面BCED | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
20.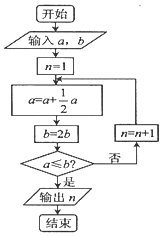 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为3,2,则输出的n=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.某班级数学兴趣小组为了研究人的脚的大小与身高的关系,随机抽测了20位同学,得到如下数据:
(Ⅰ)请根据“序号为5的倍数”的几组数据,求出y关于x的线性回归方程
(Ⅱ)若“身高大于175厘米”为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”为“大码”,“脚长小于等于42码”的为“非大码”.请根据上表数据完成2×2列联表:并根据列联表中数据说明能有多大的可靠性认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,求:抽到“无效序号(超过20号)”的概率.
附表及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}},a=\overline y-b\overline x$.
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅱ)若“身高大于175厘米”为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”为“大码”,“脚长小于等于42码”的为“非大码”.请根据上表数据完成2×2列联表:并根据列联表中数据说明能有多大的可靠性认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,求:抽到“无效序号(超过20号)”的概率.
附表及公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}},a=\overline y-b\overline x$.
17.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A. | y=$\frac{1}{x}$ | B. | y=|x|-1 | C. | y=lg x | D. | y=($\frac{1}{2}$)|x| |
15.已知集合A={x|x>-1},B={x|x2+2x-3<0}则A∩B=( )
| A. | (-1,3) | B. | (-1,1) | C. | (-1,+∞) | D. | (-3,1) |