15.以椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一动点M为圆心,1为半径作圆M,过原点O作圆M的两条切线,A,B为切点,若∠AOB=θ,θ∈[$\frac{π}{3}$,$\frac{π}{2}$],则椭圆C的离心率为( )
| A. | $\frac{\sqrt{5}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
14.若x,y满足$\left\{\begin{array}{l}{x+y≥0}\\{x≥1}\\{x-y≥0}\end{array}\right.$,则下列不等式恒成立的是( )
| A. | y≥0 | B. | x≥2 | C. | 2x-y+1≥0 | D. | x+2y+1≥0 |
13.已知正项等差数列{an}的前n项和为Sn,S10=40,则a3•a8的最大值为( )
| A. | 14 | B. | 16 | C. | 24 | D. | 40 |
12.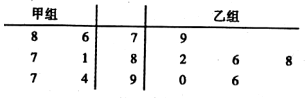 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
11.已知复数z满足z(1-i)2=1+i (i为虚数单位),则|z|为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
10.定义在(0,+∞)的函数f(x)的导函数f'(x)满足x3f'(x)+8>0,且f(2)=2,则不等式$f({e^x})<\frac{4}{{{e^{2x}}}}+1$的解集为( )
0 239182 239190 239196 239200 239206 239208 239212 239218 239220 239226 239232 239236 239238 239242 239248 239250 239256 239260 239262 239266 239268 239272 239274 239276 239277 239278 239280 239281 239282 239284 239286 239290 239292 239296 239298 239302 239308 239310 239316 239320 239322 239326 239332 239338 239340 239346 239350 239352 239358 239362 239368 239376 266669
| A. | (-∞,2) | B. | (-∞,ln2) | C. | (0,2) | D. | (0,ln2) |