题目内容
12．
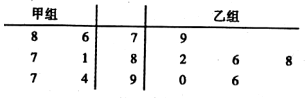以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩（单位：分），规定85分以上（含85分）为优秀，现分别从甲、乙两组中随机选取一名同学的数学成绩，则两人成绩都为优秀的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
分析 根据茎叶图中的数据，利用分步相乘原理，即可求出对应的概率值．
解答 解：根据茎叶图中的数据知，甲组85分以上（含85分）有3人，乙组有4人；
现分别从甲、乙两组中随机选取一名同学的成绩，则两人成绩都为优秀的概率是
P=$\frac{3}{6}$×$\frac{4}{6}$=$\frac{1}{3}$．
故选：B．
点评 本题考查了古典概型的概率计算问题，是基础题．
练习册系列答案
相关题目
2．已知实数x，y满足约束条件$\left\{\begin{array}{l}{x≥1，}&{\;}\\{x+y≤4，}&{\;}\\{x+by-1≤0}&{\;}\end{array}\right.$且目标函数z=x+2y最小值为1，则实数b的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，-$\frac{1}{2}$] | C． | [-$\frac{1}{2}$，0） | D． | （-∞，0）∪[2，+∞） |
3．2016年9月20日在乌鲁木齐隆重开幕的第五届中国-亚欧博览会，其展览规模为历届之最．按照日程安排，22日至25日为公众开放日．某农产品经销商决定在公众开放日开始每天以50元购进农产品若干件，以80元一件销售；若供大于求，剩余农产品当天以40元一件全部退回；若供不应求，则立即从其他地方以60元一件调剂．
（1）若农产品经销商一天购进农产品5件，求当天的利润y（单位：元）关于当天需求量n（单位：件，n∈N*）的函数解析式；
（2）农产品经销商记录了30天农产品的日需求量n（单位：件）整理得表：
若农产品经销商一天购进5件农产品，以30天记录的各需求量发生的频率作为概率，X表示当天的利润（单位：元），求X的分布列与数学期望．
（1）若农产品经销商一天购进农产品5件，求当天的利润y（单位：元）关于当天需求量n（单位：件，n∈N*）的函数解析式；
（2）农产品经销商记录了30天农产品的日需求量n（单位：件）整理得表：
| 日需求量 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 2 | 3 | 15 | 6 | 4 |
7．已知（1+x）n的展开式中第5项与第7项的二项式系数相等，则奇数项的二项式系数和为（ ）
| A． | 29 | B． | 210 | C． | 211 | D． | 212 |
4．已知全集U=Z，A={x∈Z|x2-x-2≥0}，B={-1，0，1，2}，则（∁UA）∩B=（ ）
| A． | {-1，2} | B． | {-1，0} | C． | {0，1} | D． | {1，2} |
2．已知函数f（x）是定义域R上的奇函数，且在区间[0，+∞）上单调递增，若$\frac{|f（lnx）-f（ln\frac{1}{x}）|}{2}$＜f（1），则x的取值范围为（ ）
| A． | （0，$\frac{1}{e}$） | B． | （0，e） | C． | （$\frac{1}{e}$，e） | D． | （e，+∞） |